Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Introductie van hoekpunten, zijden en diagonalen
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Introductie van hoekpunten, zijden en diagonalen eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Introductie van hoekpunten, zijden en diagonalen
Theorie
Uitdaging
Vaak zien we figuren met hoeken. Een vierhoek heeft bijvoorbeeld 4 hoekpunten en 4 zijden, een vijfhoek heeft 5 hoekpunten en 5 zijden en een zeshoek heeft 6 hoekpunten en 6 zijden.
In deze theorie leer je hoe je in vlakke figuren hoeken kunt benoemen, zijden kunt benoemen en wat een diagonaal is.
Methode
Hoekpunten
Hoekpunten in figuren geven we vaak een naam. Hiervoor gebruiken we hoofdletters zoals A, B, C en D. Neem bijvoorbeeld een vierkant met de hoeken A, B, C, en D.
Er zijn regels bedacht voor het benoemen van hoekpunten in een figuur. Je begint altijd met de letter die het eerste in het alfabet komt linksonderin te zetten. Let op! Dit hoeft niet altijd A te zijn. Je kunt ook het vierkant KLMN tekenen bijvoorbeeld. De letter K is dan de letter die het eerst in het alfabet komt.
De eerste letter zet je in een hoek linksonderin het figuur. Vervolgens ga je tegen de klok in rond het figuur en geef je de hoeken die je tegenkomst steeds de volgende letter in alfabetische volgorde.
Zijden
De hoekpunten van dit vierkant zijn met elkaar verbonden. De lijnstukken tussen de hoekpunten noem je zijden. In het vierkant ABCD zitten dus zijden AB, BC, CD en AD.
Bij het benoemen van de zijde zet je altijd de letters in alfabetische volgorde, dus AB en BC, en niet BA of CB.
Wanneer er staat: AB = 5 cm, betekent dit dat de zijde van A naar B 5 centimeter lang is.
Diagonalen
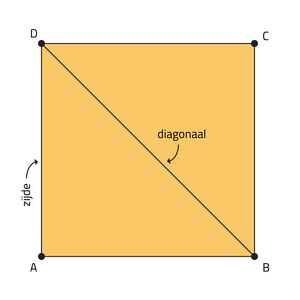
Je zou ook de hoekpunten B en D met elkaar kunnen verbinden. Je krijgt dan een lijnstuk tussen twee hoekpunten die door het figuur heen gaat. Dit noem je een diagonaal. In het vierkant ABCD kun je twee diagonalen tekenen, namelijk AC en BD.
Als je twee hoekpunten met elkaar verbindt, ontstaat er óf een zijde óf een diagonaal.
Vuistregels
- Een vierkant heeft 4 hoekpunten en 4 zijden.
- Een vijfhoek heeft 5 hoekpunten en 5 zijden.
- Een zeshoek heeft 6 hoekpunten en 6 zijden.
- Elk hoekpunt kun je benoemen met een letter. De naam van de zijde is de naam van beide hoekpunten samen.
- Twee hoekpunten die schuin tegenover elkaar liggen, kun je verbinden. De lijn die ontstaat is een diagonaal.
Voorbeeldvraag
a. Hoeveel hoekpunten kun je ontdekken?
b. Stel dat er een lijn zou lopen tussen hoekpunt A en hoekpunt D. Hoe noem je het lijnstuk AD?
c. Hoeveel zijden kun je vanuit hoekpunt C tekenen? En hoeveel diagonalen?
Uitwerking
a. Dit figuur heeft 5 hoekpunten, namelijk A, B, C, D en E.
b. Lijnstuk AD is een lijn tussen 2 hoekpunten en loopt door de figuur heen. Dit is dus een diagonaal.
c. Vanuit punt C zijn er 2 zijden, namelijk zijden BC en CD. Vanuit dit hoekpunt kun je daarnaast ook nog 2 diagonalen tekenen, namelijk AC en CE.
