Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Gevorderd - eigenschappen van hoeken
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Gevorderd - eigenschappen van hoeken eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Gevorderd - eigenschappen van hoeken
Theorie
Uitdaging
Hoeken kun je altijd opmeten, maar vaak ook berekenen. Hoeken en lijnen hebben verschillende eigenschappen die je daarbij kunnen helpen.
Methode
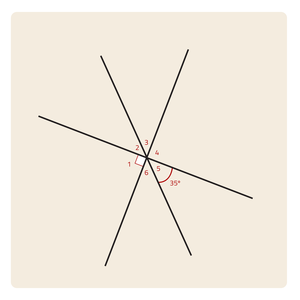
Als je een figuur hebt zoals je hier ziet kun je stap voor stap alle hoeken berekenen.
Gegeven is dat $$\angle A_{5} = 35°$$Er zijn 4 regels die helpen om de rest van de hoeken te bepalen:
- Overstaande hoeken
- Gestrekte hoek
- Rechte hoek
- Volle hoek
Overstaande hoeken
Bij 2 snijdende lijnen onstaan er 2 paar overstaande hoeken. Dit zijn de hoeken die recht tegenover elkaar liggen. Een eigenschap van overstaande hoeken is dat ze even groot zijn.
De overstaande hoek van $$\angle A_{5}$$ is $$\angle A_{2}$$. Dus moet gelden dan $$\angle A_{5} = \angle A_{2} = 35°$$
Gestrekte hoek
Een gestrekte hoek is 180°. Een voorbeeld van een gestrekte hoek in dit figuur is $$\angle A_{123}$$.
$$\angle A_{1} + \angle A_{2} + \angle A_{3} = 180°$$
Rechte hoek
In dit figuur is $$\angle A_{1}$$ een rechte hoek. Dit zie je aan het teken in de hoek. $$\angle A_{1} = 90°$$
Nu kun je met behulp van de regel van de gestrekte hoek ook $$\angle A_{3}$$ berekenen, want $$ 90° + 35° + \angle A_{3} = 180°$$. Dit geeft $$\angle A_{3} = 180° - 90° - 35° = 55°$$Ook weet je nu dankzij de regel van overstaande hoeken wat $$\angle A_{4}$$ is. $$\angle A_{4}$$ is namelijk de overstaande hoek van $$\angle A_{1}$$, en dus moet gelden $$\angle A_{4} = \angle A_{1} = 90°$$
Volle hoek
Een volle hoek is 360°. Een volle hoek zijn alle hoeken in de kruising bij elkaar. Hierdoor ontstaat een volle cirkel uit de hoeken en dit is 360°. Dus $$\angle A_{123456} = 360°$$$$\angle A_{1} = 90°$$$$\angle A_{2} = 35°$$$$\angle A_{3} = 55°$$$$\angle A_{4} = 90°$$$$\angle A_{5} = 35°$$$$\angle A_{6} = 360° - 90° - 35° - 55° - 90° - 35° = 55°$$
Vuistregels
- De som van de 3 hoeken van een driehoek is 180°
- De som van de 4 hoeken van een vierhoek is 360°
- De basishoeken van een gelijkbenige driehoek zijn gelijk aan elkaar
- Overstaande hoeken zijn gelijk aan elkaar
- Een volle hoek is 360°
- Een gestrekte hoek is 180°
- Een rechte hoek is 90°
Voorbeeldvraag
Hoe groot is $$\angle A_{3}$$?
Uitwerking
Je kunt dit op meerdere manieren uitrekenen. We geven twee verschillende oplossingen.
Manier 1:
De overstaande hoek van $$\angle A_{5}$$ is $$\angle A_{2}$$. Dus moet gelden dan $$\angle A_{5} = \angle A_{2} = 48°$$
$$\angle A_{123}$$ is een gestrekte hoek, en dus in totaal 180°, dus $$\angle A_{1} + \angle A_{2} + \angle A_{3} = 180°$$
$$\angle A_{1}$$ is een rechte hoek (van 90°) en$$\angle A_{2}$$ hadden we net bepaald met behulp van overstaande hoeken en is 48°.
We kunnen dus de formule voor de gestrekte hoek invullen: $$90° + 48° + \angle A_{3} = 180°$$
Dit geeft $$\angle A_{3} = 180° - 90° - 48° = 42°$$
Manier 2:
We weten dat een volle hoek gelijk is aan 360°, dus $$\angle A_{123456} = 360°$$
In de figuur kun je zien dat $$\angle A_{1} = 90°$$ Met behulp van overstaande hoeken weten we dan ook dat $$\angle A_{4} = 90°$$
In de figuur kun je ook zien dat $$\angle A_{5} = 48°$$ Met behulp van overstaande hoeken weten we dan ook dat $$\angle A_{2} = 48°$$
We weten nu dus dat $$\angle A_{1} = 90°$$ $$\angle A_{2} = 48°$$ $$\angle A_{4} = 90°$$ $$\angle A_{5} = 48°$$
De onbekende hoeken zijn nog $$\angle A_{3}$$ en $$\angle A_{6}$$ We rekenen nu met behulp van de volle hoek uit hoeveel graden er nog over is voor $$\angle A_{3}$$ en $$\angle A_{6}$$
$$\angle A_{123456} = 360°$$
Dit geeft $$\angle A_{3} + \angle A_{6} = 360° - \angle A_{1} - \angle A_{2} - \angle A_{4} - \angle A_{5} = 360° - 90° - 48° - 90° - 48° = 84°$$
Aangezien $$\angle A_{3}$$ en $$\angle A_{6}$$ overstaande hoeken zijn, weten we dat ze gelijk aan elkaar moeten zijn. Dat betekent dat $$\angle A_{3} = \frac{84°}{2} = 42°$$ en dat $$\angle A_{6} = \frac{84°}{2} = 42°$$
