Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
F-hoeken en Z-hoeken berekenen
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp F-hoeken en Z-hoeken berekenen eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
F-hoeken en Z-hoeken berekenen
Theorie
Uitdaging
Misschien ken je inmiddels al een aantal regels die je gebruikt bij het berekenen van hoeken. Hier bespreken we er nog 2 die je goed kunt gebruiken.
Methode
Z-hoeken
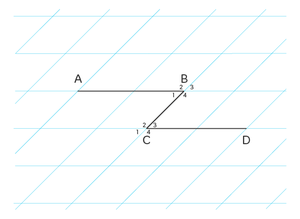
In figuren met evenwijdige lijnen kun je soms een Z herkennen. Dit zie je ook in de afbeelding genaamd Z-hoeken. De hoeken $$\angle B_{1}$$en $$\angle C_{3}$$noem je Z-hoeken. Dit zijn de hoeken aan de binnenkant van de Z. Z-hoeken zijn altijd gelijk aan elkaar. Let wel op! De lijnen AB en CD in het figuur moeten evenwijdig (of parallel) aan elkaar lopen, anders zijn er geen Z-hoeken.
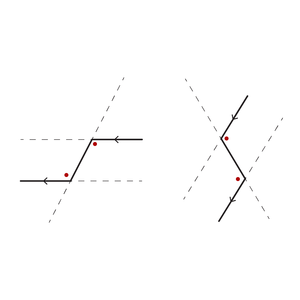
De Z-hoeken komen in verschillende vormen voor, twee andere voorbeelden zie je in de andere afbeelding.
F-hoeken
Kijk naar de afbeelding F-hoeken. De hoeken $$\angle B_{1}$$ en $$\angle C_{1}$$ zijn gelijk. Dit zijn namelijk F-hoeken. Net als Z-hoeken komen F-hoeken voor in figuren met twee evenwijdige lijnen en een lijn die deze evenwijdige lijnen snijdt of raakt. Ook F-hoeken komen in verschillende vormen voor.
Bewezen stellingen
Inmiddels ken je verschillende stellingen die je helpen bij het bereken van hoeken:
- Rechte hoek is 90°, gestrekte hoek is 180° en volle hoek is 360°
- Hoekensom driehoek = samen 180°
- Basishoeken zijn gelijk aan elkaar
- F-hoeken zijn gelijk aan elkaar
- Z-hoeken zijn gelijk aan elkaar
- Bissectrice deelt een hoek in twee gelijke hoeken.
- Z-hoeken en F-hoeken komen voor in figuren met twee evenwijdige lijnen en een lijn die deze evenwijdige lijnen snijdt of raakt.
Vuistregels
- Rechte hoek is 90°, gestrekte hoek is 180° en volle hoek is 360°
- Hoekensom driehoek = samen 180°
- Basishoeken zijn gelijk aan elkaar
- F-hoeken zijn gelijk aan elkaar
- Z-hoeken zijn gelijk aan elkaar
- Bissectrice deelt een hoek in twee gelijke hoeken.
- Z-hoeken en F-hoeken komen voor in figuren met twee evenwijdige lijnen en een lijn die deze evenwijdige lijnen snijdt of raakt.
Voorbeeldvraag
a. Welke Z-hoek uit de afbeelding hoort bij $$\angle B_{1}$$?
b. Welke F-hoek uit de afbeelding hoort bij $$\angle C_{4}$$?
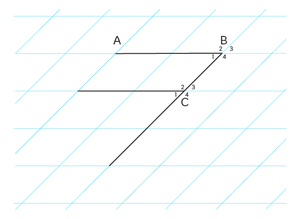
c. Gegeven is de afbeelding ΔABC. CD is de bissectrice van $$\angle C$$ en $$\angle B = 40°$$ Bereken $$\angle D_{1}$$.
Uitwerking
a. Bij $$\angle B_{1}$$ hoort de Z-hoek $$\angle C_{3}$$.
b. Bij $$\angle C_{4}$$hoort de F-hoek $$\angle B_{4}$$.
c. $$\angle A = 90°$$ (recht hoek)
$$\angle C_{12} = 180°- 40° - 90° = 50°$$ (hoekensom driehoek)
$$\angle C_{1} = \frac{50°}{2} = 25°$$ (bissectrice) $$\angle D_{1} = 180° - 90° - 25° = 65°$$ (hoekensom driehoek)
