Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Parallellogram, ruit, trapezium en vlieger
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Parallellogram, ruit, trapezium en vlieger eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Parallellogram, ruit, trapezium en vlieger
Theorie
Uitdaging
Vierhoeken zijn er in vele soorten en maten. Er bestaan een aantal speciale vierhoeken, welke specifieke eigenschappen bezitten. Zo komen we in de wiskunde en in het dagelijks leven weleens de volgende vierhoeken voor: een parallellogram, een ruit een trapezium en een vlieger.
In deze theorie behandelen we wat een parallellogram, een ruit, een trapezium en een vlieger zijn en welke eigenschappen deze figuren bezitten.
Methode
Parallellogram
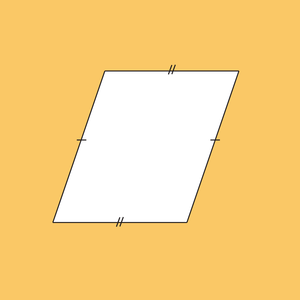
Een parallellogram is een vierhoek met bijzondere eigenschappen. De overstaande zijden van een parallellogram zijn evenwijdig en even lang. De overstaande hoeken zijn even groot en de diagonalen delen elkaar middendoor. Een parallellogram is puntsymmetrisch.
- Een figuur is puntsymmetrisch als het na een halve omwenteling hetzelfde eruit ziet als het origineel.
Ruit
Een ruit is een bijzondere parallellogram. Alle zijden van een ruit zijn namelijk even lang. De diagonalen staan loodrecht op elkaar, delen de hoeken middendoor en zijn de symmetrieassen van de ruit.
Trapezium
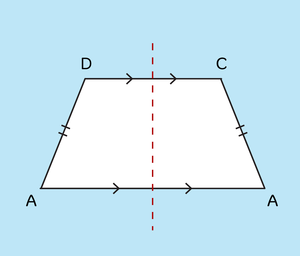
Een trapezium is een vierhoek waarvan twee zijden evenwijdig zijn. Als de niet evenwijdige zijden even lang zijn heet zo'n trapezium een gelijkbenig trapezium. Een gelijkbenig trapezium heeft één symmetrieas.
Vlieger
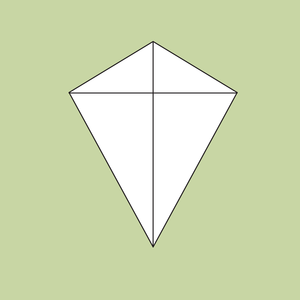
Een vierhoek waarvan één diagonaal de symmetrieas is wordt een vlieger genoemd. Een vlieger is lijnsymmetrisch.
- Een figuur is lijnsymmetrisch als je het dubbel kunt vouwen.
Vuistregels
Parallelogram
- De overstaande zijden van een parallellogram zijn evenwijdig en even lang.
- De overstaande hoeken zijn even groot en de diagonalen delen elkaar middendoor.
Ruit
- Alle zijden van een ruit zijn even lang.
- De diagonalen staan loodrecht op elkaar, delen de hoeken middendoor en zijn de symmetrieassen van de ruit.
Trapezium
- Een trapezium is een vierhoek waarvan twee zijden evenwijdig zijn.
- Als de niet evenwijdige zijden even lang zijn heet zo'n trapezium een gelijkbenig trapezium.
- Een gelijkbenig trapezium heeft één symmetrieas.
Vlieger
- Een vierhoek waarvan één diagonaal de symmetrieas is wordt een vlieger genoemd.
- Een vlieger is lijnsymmetrisch.
Symmetrie
- Een figuur is puntsymmetrisch als het na een halve omwenteling hetzelfde figuur vormt als het origineel.
- Een figuur is lijnsymmetrisch als je het dubbel kunt vouwen.
Voorbeeldvraag
In de vlieger is $$\angle A_{12} = 50°$$.
a. Welke diagonaal is de symmetrieas?
b. Hoeveel graden is $$\angle A_{1}$$?
Uitwerking
a. Diagonaal AC is de symmetrieas. Deze diagonaal deelt de vlieger in 2 gelijke delen die elkaars spiegelbeeld zijn.
b. De symmetrias AC deelt $$\angle A$$ precies door het midden. $$\angle A_{1} = \angle A_{2}$$. $$\angle A_{1} = \frac{50°}{2} = 25°$$.
