Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Bach-stelling en hpq-stelling in een driehoek
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Bach-stelling en hpq-stelling in een driehoek eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Bach-stelling en hpq-stelling in een driehoek
Theorie
Uitdaging
We kunnen de oppervlakte van $$\Delta{ABC}$$ berekenen door $$\frac{1}{2}\cdot a \cdot b $$. Ook kunnen we gebruik maken van de bach-stelling en de hpq-stelling.
In deze theorie leggen we je uit wat deze stellingen zijn en hoe je ermee kunt rekenen.
Methode
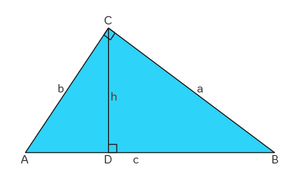
De oppervlakte van $$\Delta{ABC}$$ is op verschillende manieren te bereken. We kijken naar figuur 1.
2 manieren zijn:
- $$\frac{1}{2} · a · b $$
- $$\frac{1}{2} · c · h $$
De bach-stelling
Omdat je met beide manieren de oppervlakte berekent, zou je kunnen zeggen dat:
$$\frac{1}{2} · b · a $$ = $$\frac{1}{2} · c · h $$, oftewel b · a = c · h
Dit wordt ook wel de bach-stelling genoemd. Door de bekende getallen in te vullen kun je een van de variabelen berekenen.
- b en a zijn de zijdes van de loodrechte hoek.
- c is de langste zijde.
- h is de hoogte die loodrecht op zijde c staat.
Bijvoorbeeld b, a en c zijn bekend. Dan kun je door deze in te vullen, h berekenen.
Stel b = 2, a = 4, c = 4.
2 · 4 = 4 · h
4 · h = 8 $$ h = \frac{8}{4} = 2 $$
De hpq-stelling
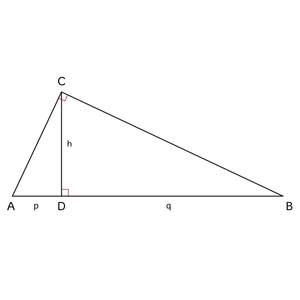
In rechthoekige driehoeken is h2= p · q. Dit wordt de hpq-stelling genoemd.
Door deze in te vullen kun je h, p of q berekenen.
Vuistregels
- bach-stelling: b · a = c · h
- hpq-stelling: h2 = p · q
- b en a zijn de zijdes van de loodrechte hoek.
- c is de langste zijde.
- h is de hoogte die loodrecht op zijde c staat.
Voorbeeldvraag
a. Zie Figuur 1. Bereken de hoogte LN in cm. Rond af op 1 decimaal.
b. Zie Figuur 2. Bereken PQ. Rond af op 1 decimaal.
Uitwerkingen:
a. bach-stelling: b · a = c · h
b = 7,5 ; a = 3,2 ; c = 8,2 ; h = LN
3,2 · 7,5 = 8,2 · LN.
24 = 8,2 · LN
$$LN = \frac{24}{8,2} = 2,9$$
b. hpq-stelling: h2= p · q, dus NQ2 = OQ · PQ
52 = 6,7 · PQ $$PQ = \frac {25}{6,7} = 3,7$$
