Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Stelling van Pythagoras - schuine zijde berekenen en toepassen in een assenstelsel
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Stelling van Pythagoras - schuine zijde berekenen en toepassen in een assenstelsel eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Stelling van Pythagoras - schuine zijde berekenen en toepassen in een assenstelsel
Theorie
Uitdaging
In een rechthoekige driehoek kun je de schuine zijde berekenen met behulp van de Stelling van Pythagoras. Ook kun je de lengte van een schuine lijn in een assenstelsel berekenen met behulp van Pythagoras.
Hoe je deze dingen aanpakt behandelen we in deze theorie.
Methode
Schuine zijde
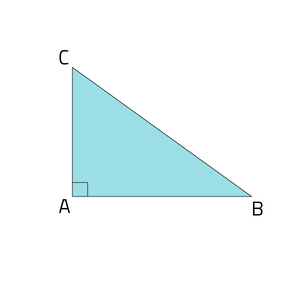
In een rechthoekige driehoek is de schuine zijde te berekenen als beide rechthoekszijden gegeven zijn. Je gebruikt hier de stelling van Pythagoras voor. Bij ΔABC is $$\angle B = 90°$$. De stelling van Pythagoras voor deze driehoek is AB2 + BC2 = AC2. Als je de lengte van zijde AB en zijde BC weet, kun je de lengte van schuine zijde AC berekenen.
Assenstelsel
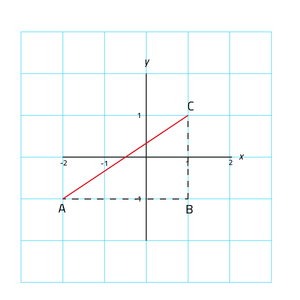
Om afstanden tussen twee punten in een assenstelsel te berekenen maak je gebruik van hetzelfde principe. Om de afstand in de afbeelding 'Assenstelsel' tussen A(-2,-1) en C(1,1) te berekenen, kun je gebruik maken van het denkbeeldige punt B waardoor je de rechthoekige driehoek ABC krijgt. Vervolgens gebruik je de Stelling van Pythagoras om AC te berekenen. Zijde AB en BC zijn de rechthoekszijden en deze kun je aflezen in het assenstelsel. Zijde AC is de schuine zijde en deze bereken je met de stelling van Pythagoras: AB2 + BC2 =AC2.
Let op dat $$\angle B = 90°$$.
Vuistregels
- Je kunt de Stelling van Pythagoras toepassen in rechthoekige driehoeken
- Stelling van Pythagoras: (ene rechthoekszijde)2 + (andere rechthoekszijde)2 = (schuine zijde)2
- Of ook wel bekend als: a2 + b2 = c2, waarbij a en b de rechthoekszijden zijn en c de schuine zijde is
- Om de afstand van een lijnstuk in een assenstelsel te berekenen, kun je gebruik maken van een denkbeeldige punt waardoor je een rechthoekige driehoek krijgt en daardoor de Stelling van Pythagoras kunt gebruiken.
Voorbeeldvraag
In ΔABC is $$\angle B = 90°$$, AB = 8 cm en BC = 3 cm. Bereken AC. Rond af op 1 decimaal.
Uitwerking
Tip! Teken de driehoek voordat je begint met rekenen.
AB2 + BC2 = AC2 (Stelling van Pythagoras)
82 + 32 = AC2
64 + 9 = AC2
AC2 = 73 $$AC = \sqrt{73} \approx 8,5 \mbox{ cm}$$.
