Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Zijden benoemen van rechthoekige driehoeken
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Zijden benoemen van rechthoekige driehoeken eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Zijden benoemen van rechthoekige driehoeken
Theorie
.png)
Uitdaging
In plaats van de verticale verplaatsing en de horizontale verplaatsing, hebben we het in driehoeken ook wel over de overstaande rechthoekzijde en de aanliggende rechthoekzijde.
Elke driehoek heeft 3 zijden. De schuine zijde (ook wel de langste zijde genoemd) ligt ALTIJD tegenover de rechte hoek. De zijden die aan de rechte hoek vast zitten heten de rechthoekzijden. Je weet pas wat de overstaande rechthoekzijde of de aanliggende rechthoekzijde is als je weet vanuit welke hoek je moet kijken.
Methode
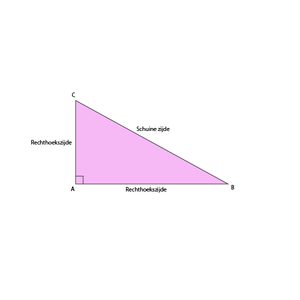
In de afbeelding zie je rechthoekige driehoek $$\triangle ABC$$.
De rechthoekszijden zijn de zijden die aan de rechte hoek liggen. Bij deze driehoek is $$\angle A$$ de rechte hoek. De rechthoekszijden zijn dus zijde $$AB$$ en zijde $$AC$$.
De schuine zijde is de zijde die tegenover de rechte hoek ligt. Bij deze driehoek is dat zijde $$BC$$.
In de andere afbeelding zie je rechthoekige driehoek $$\triangle DEF$$.
In deze driehoek is $$\angle F$$ de rechte hoek. Zijde $$DF$$ en zijde $$EF$$ zijn de rechthoekszijden en zijde $$DE$$ is de schuine zijde.
Rechthoekszijde $$DF$$ is een been van $$\angle D$$ en heet daarom de aanliggende rechthoekszijde van $$\angle D$$.
Rechthoekszijde $$EF$$ ligt tegenover $$\angle D$$ en heet daarom de overstaande rechthoekszijde van $$\angle D$$.
Op deze manier kan je ook zien dat rechthoekszijde $$EF$$ de aanliggende rechthoekszijde van $$\angle E$$ is en dat rechthoekszijde $$DF$$ de overstaande rechthoekszijde is van $$\angle E$$.
LET OP: JE KIJKT NOOIT VANUIT DE RECHTE HOEK!
Vuistregels
- De schuine zijde ligt tegenover de rechte hoek.
- Rechthoekszijden zijn benen van de rechte hoek.
Voorbeeldvraag
a. Wat is de aanliggende rechthoekszijde van $$\angle M$$ in $$\triangle KLM$$?
b. Wat is de schuine zijde van $$\triangle NOP$$?
c. Wat is de overstaande rechthoekszijde van $$\angle S$$ in $$\triangle RST$$?
Uitwerking:
a. Zijde $$KM$$ is de aanliggende rechthoekszijde van $$\angle M$$. $$\angle K$$ is de rechte hoek en zijde $$KM$$ en zijde $$KL$$ zijn dus rechthoekzijden. $$KM$$ is een been van $$\angle K$$ en is dus de aanliggende rechthoekszijde van $$\angle K$$.
b. Zijde $$NO$$ is de schuine zijde. $$\angle P$$ is de rechte hoek. Zijde $$NO$$ ligt tegenover $$\angle P$$ en is dus de schuine zijde.
c. Zijde $$RT$$ is de overstaande rechthoekszijde van $$\angle S$$. $$\angle R$$ is de rechte hoek en zijde $$RT$$ en zijde $$RS$$ zijn dus rechthoekszijden. $$RT$$ ligt tegenover $$\angle S$$ en is dus de overstaande rechthoekszijde van $$\angle S$$.
