Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Kwartielen en de kwartielafstand
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Kwartielen en de kwartielafstand eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Kwartielen en de kwartielafstand
Theorie
Uitdaging
Als je een serie waarnemingsgetallen hebt, kun je de mediaan berekenen om te weten hoe de waarnemingen ongeveer verdeeld zijn.
De mediaan alleen geeft echter niet zoveel informatie over de getallenreeks. Daarom wordt er bij waarnemingenreeksen ook weleens gebruik gemaakt van kwartielen. Met deze kwartielen kun je nog beter zien hoe de waarnemingen verspreid zijn.
In deze theorie gaan we in op kwartielen en de kwartielafstand.
Methode
Als je iets waarneemt en daar de waarden van opschrijft, krijg je een waarnemingsreeks. Het is lastig om iets te zeggen over een verzameling getallen. Je kunt rekenen met de waarnemingsgetallen om meer te weten te komen hoe de getallen verdeeld zijn.
Een van de manieren om te begrijpen hoe een verzameling getallen verdeeld is is met behulp van de mediaan. De mediaan is het middelste getal van de waarnemingsreeks als deze van laag naar hoog gesorteerd is. Als de reeks bestaat uit een even aantal getallen is de mediaan het gemiddelde van de middelste 2 getallen.
Voor de 2 helften die door de mediaan verdeeld zijn kunnen weer een nieuwe mediaan bepaald worden. Je krijgt dan 4 groepen die alle 4 bestaan uit (ongeveer) 25% van het aantal getallen in de waarnemingsreeks. De mediaan over de eerste helft (met de laagste getallen) heet het eerste kwartiel en wordt aangegeven met Q1. De mediaan over de tweede helft (met de hoogste getallen) heet het derde kwartiel en wordt aangegeven met Q3. Dit heet het derde kwartiel omdat 3 kwart van de getallen lager dan (of gelijk aan) dit getal zijn.
Q1 en Q3 worden berekend op dezelfde manier als de mediaan. Als de waarnemingsreeks uit een oneven aantal bestaat wordt de mediaan zelf niet meegerekend bij een helft. De 2 helften zijn daarom altijd even groot. Als een helft uit een oneven aantal bestaat is het middelste getal het kwartiel. Als een helft uit een even aantal bestaat is het kwartiel het gemiddelde van de middelste 2 getallen.
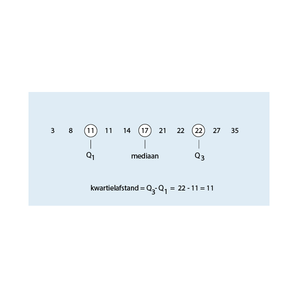
De kwartielafstand is het verschil tussen het eerste kwartiel en het derde kwartiel:
Kwartielafstand = Q3 - Q1
De kwartielafstand geeft aan hoe verspreid de getallen in de waarnemingsreeks zijn. De kwartielafstand is daarom een voorbeeld van een spreidingsmaat.
Vuistregels
- De mediaan verdeeld een waarnemingsreeks die van laag naar hoog geordend is in 2 even grootte groepen.
- Het eerste kwartiel, Q1, verdeelt de eerste helft in 2 gelijke groepen.
- Het derde kwartiel, Q3, verdeelt de tweede helft in 2 gelijke groepen.
- Kwartielafstand = Q3 - Q1
Voorbeeldvraag
Bij de gymles moeten de leerlingen van H3C zo vaak als ze kunnen een voetbal hooghouden. De aantallen zijn bijgehouden door de gymdocent.
2, 67, 33, 12, 5, 2, 4, 9, 1, 19, 11, 10, 20
a. Bereken de mediaan.
b. Bereken het eerste en het derde kwartiel.
Uitwerking:
a. Je kunt de mediaan berekenen in 2 stappen.
- Stap 1: Zet de getallen in volgorde van klein naar groot.
1, 2, 2, 4, 5, 9, 10, 11, 12, 19, 20, 33, 67
- Stap 2: Vind het middelste getal.
De mediaan is 10.
b. Bereken het eerste en derde kwartiel.
- Stap 1: Verdeel de reeks in 2 gelijke helften.
Omdat de waarnemingsreeks bestaat uit een oneven aantal getallen tel je de mediaan (10) niet mee bij de helften.
Eerste helft op volgorde: 1, 2, 2, 4, 5, 9
Tweede helft op volgorde: 11, 12, 19, 20, 33, 67
- Stap 2: Vind het middelste getal.
De helften bestaan uit een even getal. Het kwartiel is in dit geval het gemiddelde van de middelste 2 getallen.
$$Q_1 = \frac{2 + 4}{2} = 3$$ $$Q_3 = \frac{19 + 20}{2} = 19,5$$
