Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Meerdere procentuele veranderingen omrekenen
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Meerdere procentuele veranderingen omrekenen eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Meerdere procentuele veranderingen omrekenen
Theorie
Uitdaging
Het komt soms voor dat je de procentuele verandering over een bepaalde tijd wilt weten, maar er binnen die tijd verschillende procentuele veranderingen hebben plaatsgevonden. Je moet die dan om kunnen rekenen naar één procentuele verandering.
Hoe je dit kunt doen leggen we je uit in deze theorie.
Methode
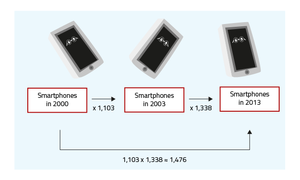
Stel je voor dat het smartphonegebruik tussen 2000 en 2003 is toegenomen met 10,3% en tussen 2003 en 2013 met 33,8%. Je weet nu de procentuele toename van het smartphonegebruik, maar van 2 verschillende periodes. Hoe bereken je nu de procentuele toename tussen 2000 en 2013 aan de hand van deze gegevens?
Eerst zet je de procentuele toe- of afname om in een vermenigvuldigingsfactor. Bij een toename van 10,3% hoort een vermenigvuldigingsfactor van 1,103 en bij een toename van 33,8% een vermenigvuldigingsfactor van 1,338.
De totale procentuele toename tussen 2000 en 2013 bereken je door de 2 vermenigvuldigingsfactoren met elkaar te vermenigvuldigen. In het voorbeeld van het smartphonegebruik bereken je de totale procentuele toename dus zo:
- Totale procentuele toename = 1,103 · 1,338 = 1,475.. $$\approx{1,476}$$
Bij een vermenigvuldigingsfactor van 1,476 hoort een procentuele toename van 47,6%.
Het smartphonegebruik is tussen 2000 en 2013 dus toegenomen met 47,6%.
Je kunt de vermenigvuldigingsfactoren van verschillende periodes eindeloos met elkaar vermenigvuldigen om de toe- of afname over een langere periode te berekenen.
Tenzij anders gevraagd geef je procenten altijd in 1 decimaal nauwkeurig!
Vuistregels
- Voor de vermenigvuldigingsfactor van een totale toe- of afname vermenigvuldig je alle aparte vermenigvuldigingsfactoren met elkaar
- Bij een vermenigvuldigingsfactor van 1,1 hoort een toename van 10%
- Bij een vermenigvuldigingsfactor van 0,9 hoort een afname van 10%
Voorbeeldvraag
a. Tussen 2008 en 2010 is het aantal geboortes in Nederland gestegen met 3,7% en vanaf 2010 tot en met 2013 nog eens met 4,5%. Met hoeveel procent is het aantal geboortes gestegen in de periode 2008-2013?
b. In de periode van 1993 tot en met 2001 groeide de cola consumptie met 2,5%. In 2005 was dit alweer 1,2% meer dan in 2001. In de periode 2005-2010 daalde de consumptie weer met een halve procent. Wat was de procentuele toe- of afname in de periode 1993-2010?
Uitwerking
a. 1,037 · 1,045 = 1,083.. $$\approx{1,084}$$. Hier hoort een toename bij van 8,4%.
b. 1,025 · 1,012 · 0,995 = 1,032.. $$\approx{1,032}$$. Hier hoort een toename bij van 3,2%.
