Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Bissectrices en de ingeschreven cirkel
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Bissectrices en de ingeschreven cirkel eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Bissectrices en de ingeschreven cirkel
Theorie
Uitdaging
Een hoek kun je precies door midden delen waardoor de hoek gesplitst wordt in twee even grote hoeken. De lijn die de hoek door midden deelt heet een bissectrice. De ingeschreven cirkel raakt alle zijden van de driehoek (en snijdt deze dus niet).
Je kunt de ingeschreven cirkel tekenen met behulp van de bissectrices van de driehoek. Hoe dat precies werkt wordt in deze theorie besproken.
Methode
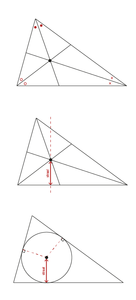
De bissectrice deelt een hoek in 2 gelijke hoeken en heeft als eigenschap dat de afstand van elk punt op de bissectrice even ver ligt van beide benen van de hoek. Je kunt in een driehoek 3 bissectrices tekenen, vanuit elke hoek eentje.
Het punt waar de bissectrices elkaar snijden heeft als speciale eigenschap dat de afstand tot alle 3 de zijden van de driehoek gelijk is. Dit is dus het middelpunt van de driehoek.
Je kunt een cirkel om dit middelpunt tekenen met als straal de kortste afstand tot de zijden van de driehoek. Deze cirkel heet de ingeschreven cirkel van de driehoek. Deze cirkel raakt alle zijden van de driehoek en heeft als middelpunt het snijpunt van de bissectrices.
Je kunt een ingeschreven cirkel tekenen. Begin hiervoor met het tekenen van de 3 bissectrices van de driehoek. Dit kun je doen met behulp van je passer en geodriehoek. Het snijpunt van de bissectrices is het middelpunt van de ingeschreven cirkel. De straal van de ingeschreven cirkel is de kortste afstand tussen het middelpunt en één van de zijden. Dit kun je vinden door de loodlijn van één van de zijden te tekenen, die door het middelpunt gaat.
Vervolgens stel je je passer in op deze straal en teken je de ingeschreven cirkel.
Vuistregels
- Een bissectrice deelt een hoek precies doormidden.
- Een ingeschreven cirkel raakt de 3 zijden van een driehoek.
- Een ingeschreven cirkel heeft als middelpunt het snijpunt van de bissectrices van de hoeken.
Voorbeeldvraag
Je hebt driehoek ABC, zie afbeelding. Teken de bissectrices van ∠A en ∠B.
a. Teken een cirkel met als middelpunt het snijpunt van beide bissectrices met een straal die precies zijde AB raakt. Wat valt je op?
b. Hoe noem je het snijpunt van de bissectrices?
c. Teken de bissectrice van ∠C. Wat valt je op?
Uitwerking:
a. De cirkel raakt precies alle zijden van de driehoek, niet alleen zijde AB.
b. Het middelpunt van de ingeschreven cirkel.
c. De bissectrice van ∠C snijdt precies door het snijpunt van de andere twee bissectrices, het middelpunt van de ingeschreven cirkel.
