Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Bissectrice
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Bissectrice eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Bissectrice
Theorie
Uitdaging
De bissectrice is een speciale lijn met specifieke eigenschappen. Door de bissectrice te tekenen kun je ook wat zeggen over afstanden in de figuur.
Wat een bissectrice precies is en hoe je deze kunt tekenen leggen we je uit in deze theorie.
Methode
Een hoek kun je precies door midden delen waardoor de hoek gesplitst wordt in twee even grote hoeken.
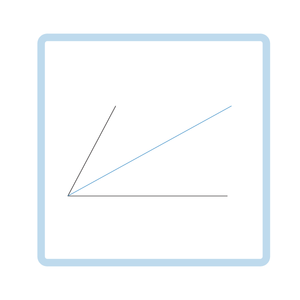
De lijn die de hoek door midden deelt heet een bissectrice. In de afbeelding is dit de blauwe lijn.
Elk punt op de bissectrice heeft dezelfde afstand tot beide benen van de hoek. Dus als er een punt in een driehoek op gelijke afstand ligt van beide benen van de hoek, dan ligt dit punt op de bissectrice.
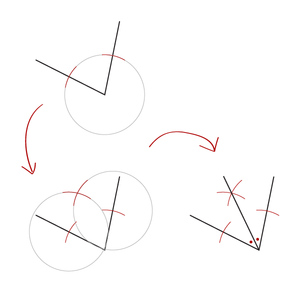
Een bissectrice kun je tekenen met behulp van je passer en je geodriehoek. Zet de benen van je passer een stukje uit elkaar, het maakt niet uit hoever dit is, maar zorg er in ieder geval dat je het niet verder uit elkaar zet dan de lengte van de benen van de hoek in de figuur. Zet de passerpunt in de hoek en teken een cirkel. Je hebt alleen de stukjes van de cirkel nodig, waar deze de benen van de hoek snijdt, je kunt dus ook alleen deze stukjes tekenen.
Vervolgens teken je vanaf beide snijpunten weer twee nieuwe cirkels. Het maakt weer niet uit hoever de benen van je passer uit elkaar staan, als je er maar wel voor zorgt dat de twee cirkels elkaar snijden. Vervolgens kun je een lijn trekken vanuit de hoek door dit snijpunt. Dit is de bissectrice.
Vuistregels
- Een bissectrice deelt een hoek in twee gelijke hoeken.
- Elk punt op de bissectrice ligt op gelijke afstand van beide benen van de hoek.
Voorbeeldvraag
Teken de punten die binnen vierhoek ABCD even ver van de benen van $$\angle C$$ liggen en een afstand hebben tot C van meer dan 2.
Uitwerking:
Je wilt de punten die even ver van de benen van hoek C liggen, dus de bissectrice van $$\angle C$$. Daarnaast moeten de punten ook op een afstand van meer dan 2 van $$\angle C$$ af liggen. Hiervoor teken je een cirkel om punt C. Het antwoord is dan alle punten op de bissectrice die buiten de cirkel en binnen de vierhoek liggen. Dit is dus het rode gedeelte van de lijn.
