Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Oppervlakte van samengevoegde vlakke figuren
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Oppervlakte van samengevoegde vlakke figuren eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Oppervlakte van samengevoegde vlakke figuren
Theorie
.png)
Uitdaging
Sommige vlakke figuren hebben niet duidelijk één vorm waardoor de oppervlakte niet met een enkele formule te berekenen is. In zulke gevallen is het handig om de figuur op te delen in stukken. Zo houdt je vervolgens verschillende figuren over die we kennen en waar we formules voor bedacht hebben om de oppervlakte ervan te kunnen berekenen.
Hoe je zo'n vlakke figuur zonder duidelijk herkenbare vorm kunt opdelen en de oppervlakte van die figuur kunt berekenen, bespreken we in deze theorie.
Methode
Als we een figuur in stukken opdelen kun je elk stuk benoemen en de oppervlakte los berekenen. Zo krijg je bijvoorbeeld oppervlakte I, oppervlakte II en oppervlakte III.
De totale oppervlakte krijg je door deze bij elkaar op te tellen.
Totale oppervlakte = oppervlakte I + oppervlakte II + oppervlakte III.
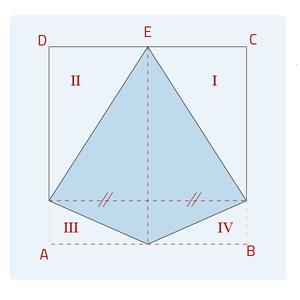
Sommige figuren zijn lastiger. Als we de oppervlakte van de vlieger in het voorbeeld willen berekenen kunnen we dat als volgt doen:
- We berekenen de oppervlakte van het hele vlak waarin de vlieger ligt. We noemen dit bijvoorbeeld oppervlakte ABCD.
- We gaan de oppervlaktes van de driehoeken die om de vlieger heen liggen van oppervlakte ABCD aftrekken. Dan houden we de oppervlakte van de vlieger over. We noemen deze oppervlaktes I, II, III en IV.
- Oppervlakte vlieger = Oppervlakte ABCD - Oppervlakte I - Oppervlakte II - Oppervlakte III - Oppervlakte IV
Let op, dit voorbeeld kan ook sneller met de formule:
- $$\mbox{Oppervlakte vlieger} = \frac{1}{2} · \mbox{lengte diagonaal} · \mbox{breedte diagonaal}$$
Op dezelfde manier zou je de oppervlakte van de rechter figuur kunnen berekenen.
Vuistregels
- $$\mbox{Oppervlakte rechthoek = lengte · breedte}$$
- $$\mbox{Oppervlakte parallellogram = zijde · bijbehorende hoogte}$$
- $$\mbox{Oppervlakte trapezium}= \frac{1}{2} · \mbox{som evenwijdige zijden} · \mbox{ bijbehorende hoogte}$$
- $$\mbox{Oppervlakte vlieger} = \frac{1}{2} · \mbox{lengte diagonaal} · \mbox{breedte diagonaal}$$
Voorbeeldvraag
Bereken de oppervlakte van de vlieger.
Uitwerking
We berekenen de oppervlakte van de vlieger door oppervlakte I, II, III en IV van oppervlakte ABCD af te trekken.
Omdat een vlieger symmetrisch is weten we dat de lengte CE gelijk is aan DE. En dat oppervlaktes I en II gelijk zijn en de oppervlaktes III en IV.
Oppervlakte ABCD = lengte · breedte = (10 + 3) · (7 + 7) = 13 · 14 = 182
$$\mbox{Oppervlakte I = Oppervlakte II} = \frac{1}{2} · 10 · 7 = 35 $$
$$\mbox{Oppervlakte III = Oppervlakte IV} = \frac{1}{2} · 3 · 7 = 10,5 $$
Oppervlakte I + Oppervlakte II + Oppervlakte III + Oppervlakte IV = 35 + 35 + 10,5 + 10,5 = 91
Oppervlakte vlieger = 182 - 91 = 91
Deze vraag zou zelfs nog sneller kunnen worden berekend:
$$\mbox{Oppervlakte vlieger} = \frac{1}{2} · \mbox{lengte diagonaal} · \mbox{breedte diagonaal}$$ $$\mbox{Oppervlakte vlieger} = \frac{1}{2} · 13 · 14 = 91$$
