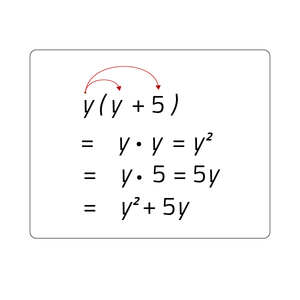Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Ontbinden in factoren - één gemeenschappelijke factor
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Ontbinden in factoren - één gemeenschappelijke factor eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Ontbinden in factoren - één gemeenschappelijke factor
Theorie
Uitdaging
Als je 12x2a in zoveel mogelijk factoren wil ontbinden, krijg je het volgende: 2 · 2 · 3 · x · x · a
Soms is het overzichtelijker om haakjes te gebruiken om een formule op te schrijven. Om dit te doen moet je een gemeenschappelijke factor herkennen en buiten haakjes brengen.
Hoe dit 'ontbinden in factoren' precies werkt leggen we je uit in deze theorie.
Methode
Voorbeeld: y2 + 5y kan je ook schrijven als y · (y + 5). Je mag hierbij het keerteken weglaten: y(y + 5) Je maakt van een optelsom een vermenigvuldigsom. We noemen dit ook wel ontbinden in factoren.
Hoe ga je te werk?
- Stap 1: Bepaal uit welke verschillende termen de som bestaat.
- Stap 2: Bepaal welke factor in beide termen voorkomt: de gemeenschappelijke factor.
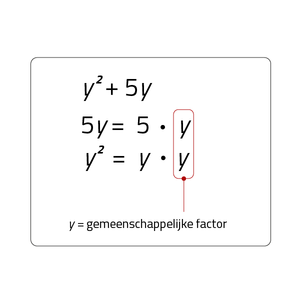
5y = 5 · y en y2= y · y. In dit geval is dus y de gemeenschappelijke factor, deze plaats je dus voor de haakjes y(.....). De rest blijft over voor binnen de haakjes: y en 5.
De formule wordt dus: y(y + 5).
- Stap 3: Je kan het antwoord controleren door terug te rekenen: y · y = y2 en y · 5 = 5y, zo zijn we weer terug bij onze begintermen.
We noemen dit ontbinden in factoren. Je ontbindt namelijk de som in losse factoren.
Vuistregels
Hoofdregels:
- y2 + 5y = y(y + 5)
- De gemeenschappelijke factor is y.
- De gemeenschappelijke factor halen we buiten de haakjes.
Voorbeeldvraag
Ontbind de volgende formule in factoren:
6x2+ 7x
Uitwerking
- Stap 1. Deze som bevat de termen 6x2 en 7x
- Stap 2. Zoek eerst de gemeenschappelijke factor van deze 2 delen.
6x2= 6 · x · x en 7x = 7 · x
Beide delen bevatten de factor x. Dit is dus de factor die buiten de haakjes komt te staan. Voor binnen de haakjes houdt je over: 6x en 7
De formule wordt dus: 6x2+ 7x = x(6x + 7)
- Stap 3. Dit kun je controleren door terug te rekenen.
