Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Berekeningen met de Stelling van Pythagoras
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Berekeningen met de Stelling van Pythagoras eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Berekeningen met de Stelling van Pythagoras
Theorie
Uitdaging
In een rechthoekige driehoek kun je de schuine zijde berekenen met behulp van de Stelling van Pythagoras. Daarnaast kun je ook de rechthoekszijden berekenen met de Stelling van Pythagoras.
Hoe je berekeningen uitvoert met de Stelling van Pythagoras wordt in deze theorie behandeld.
Methode
In een rechthoekige driehoek is een zijde te berekenen als beide andere zijden gegeven zijn. Je gebruikt hiervoor de Stelling van Pythagoras:
(ene rechthoekszijde)2 + (andere rechthoekszijde)2 = (schuine zijde)2
Of ook wel bekend als: a2 + b2 = c2, waarbij a en b de rechthoekszijden zijn en c de schuine zijde is.
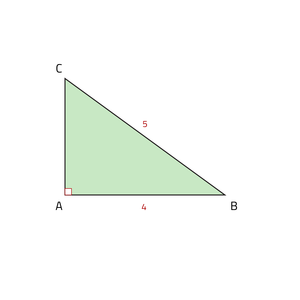
Bij ΔABC is $$\angle A = 90°$$. De stelling van Pythagoras voor deze driehoek is AB2 + AC2 = BC2. Als je de lengte van zijde AB en zijde BC weet, kun je de lengte van zijde AC berekenen.
42 + AC2 = 52
16 + AC2 = 25
AC2 = 25 - 16 = 9 $$AC = \sqrt{9} = 3$$
De stelling van Pythagoras kun je alleen gebruiken bij een rechthoekige driehoek.
Als je van een driehoek de lengte van alle zijden weet, dan kun je nagaan of deze driehoek een rechthoekige driehoek is. Je moet dan de gegevens in de stelling van Pythagoras invullen. Klopt deze som? Dan heb je een rechthoekige driehoek. Klopt deze som niet? Dan heeft deze driehoek geen rechte hoek.
Vuistregels
- Je kunt de Stelling van Pythagoras toepassen in rechthoekige driehoeken
- Stelling van Pythagoras: (ene rechthoekszijde)2 + (andere rechthoekszijde)2 = (schuine zijde)2
- Of ook wel bekend als: a2 + b2 = c2, waarbij a en b de rechthoekszijden zijn en c de schuine zijde is
Voorbeeldvraag
a. Bereken zijde KL in ΔKLM. Rond af op 1 decimaal.
b. Is ΔABC een rechthoekige driehoek?
c. Is ΔDEF een rechthoekige driehoek?
Uitwerking
a. ΔKLM is een rechthoekige driehoek, want $$\angle K = 90°$$.
Zijden KL en KM zijn de rechthoekszijden en zijde LM is de schuine zijde.
KL2 + KM2 = LM2(stelling van Pythagoras)
KL2 + 52 = 92
KL2 = 81 - 25 = 56
$$KL = \sqrt{56} \approx 7,5$$
b. Allereerst bekijk je welke zijde het langst is, dit is de schuine zijde. Als er een rechte hoek in de driehoek zit, dan zou dit alleen de hoek tegenover de schuine zijde kunnen zijn. Zijde AC is de langste zijde. De stelling van Pythagoras wordt dan:
(ene rechthoekszijde)2 + (andere rechthoekszijde)2 = (schuine zijde)2
AB2 + BC2 = AC2
32 + 42 = 52
9 + 16 = 25
De formule klopt voor ΔABC en dus is dit een rechthoekige driehoek.
c. De langste zijde is zijde DE, wat in de Stelling van Pythagoras de schuine zijde zou zijn. De stelling van Pythagoras wordt dan:
(ene rechthoekszijde)2 + (andere rechthoekszijde)2 = (schuine zijde)2
DF2 + EF2 = DE2
62 + 42 $$\neq$$ 82, want 16 + 36 $$\neq$$ 64
Deze som klopt niet. En dus is ΔDEF geen rechthoekige driehoek.
