Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Lijndiagrammen
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Lijndiagrammen eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Lijndiagrammen
Theorie
Uitdaging
In de statistiek hebben we vaak te maken met verschillende gegevens, zoals meetresultaten. Diagrammen worden gebruikt om op een overzichtelijke manier deze informatie weer te geven.
Eén van de diagrammen die regelmatig wordt gebruikt is het lijndiagram. In deze theorie leggen we uit wat een lijndiagram is en hoe je deze kunt aflezen en tekenen.
Methode
Een lijndiagram bestaat uit stippen die verbonden worden door een lijn. Elke stip in het assenstelsel geeft een meting weer. Als je gegevens beginnen met een hoge waarde op de y-as, dan kun je een scheurlijn gebruiken. Door middel van een scheurlijn kan je de waardes op de y-as direct met hoge getallen laten beginnen.
Aflezen
- Om te weten wat een lijn weergeeft moet je naar de (horizontale) x-as, de titel van de diagram of de legenda kijken.
- Om te weten wat de waarde van de verschillende punten op een lijn in een lijndiagram is, kijk je naar de (verticale) y-as.
Tekenen
- Stap 1: Zet de juiste informatie op de x-as en y-as.
- Stap 2: Zet voor elke bekende waarde op de x-as een punt ter hoogte van de bijbehorende waarde op de y-as.
- Stap 3: Verbind de stippen met een lijn.
- Stap 4: Als de lijndiagram meerdere lijnen bevat, maak er dan een legenda bij, zodat duidelijk is welke lijn welke informatie weergeeft.
Vuistregels
- $$\mbox{Een lijndiagram bestaat uit stippen die verbonden worden door een lijn}$$
- $$\mbox {Procentuele toename} = \frac{\mbox{nieuw - oud}}{\mbox{oud}} · 100\%$$
Voorbeeldvraag
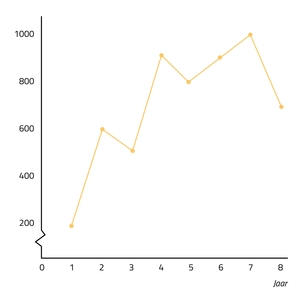
In de afbeelding is een lijndiagram te zien. In de lijndiagram is op de y-as het aantal verkochte kilo's tulpen te zien van het bedrijf Tulip BV. Op de x-as is het aantal jaar te zien dat het bedrijf bestaat.
a. Na hoeveel jaar verkocht Tulip BV. 900 kilo tulpen?
b. Hoeveel procent was dat meer ten opzichte van het vorige jaar?
Uitwerking
a. In de lijndiagram is te zien dat er 900 kilo is verkocht in het 4de jaar dat het bedrijf bestaat.
b. Het vorige jaar is het 3de jaar. Toen is er 500 kilo verkocht. We willen weten hoeveel procent het aantal is toegenomen.
3de jaar (oud) = 500 kilo, 4de jaar (nieuw) = 900 kilo.
Toename = nieuw - oud = 900 - 500 = 400 kilo.
$$\mbox {Procentuele toename} = \frac{\mbox{nieuw - oud}}{\mbox{oud}} · 100\%$$ $$\mbox{Procentuele toename =} \frac{400}{500} · 100\% = 80\% $$
