Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Spiegelen in de ruimte
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Spiegelen in de ruimte eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Spiegelen in de ruimte
Theorie
.png)
Uitdaging
Symmetrie bestaat in vele vormen. Zo is ook deze kubus symmetrisch. In een plat symmetrisch voorwerp, zoals een vlieger, is er een lijn die het figuur in 2 gelijke delen deelt, de symmetrieas. In een 3-D voorwerp, zoals deze kubus, is dit niet een lijn, maar een vlak.
Hoe dit precies zit behandelen we in deze theorie.
Methode
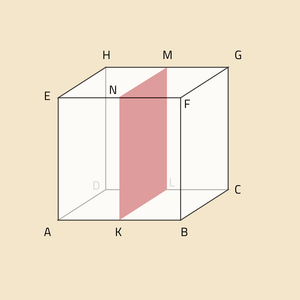
In de kubus zie je het vlak KLMN. Dit vlak heet het symmetrievlak van de kubus. Dit vlak stelt een spiegel voor: het deelt de kubus in 2 gelijke delen die elkaars spiegelbeeld zijn.
Het spiegelbeeld van punt E is punt F. En het spiegelbeeld van ribbe AD is ribbe BC.
Een kubus heeft meerdere symmetrievlakken. Er zijn dus meerdere manieren waarop je de kubus in tweeën kunt delen, wat 2 gelijke delen oplevert die elkaar spiegelbeeld zijn. In de afbeelding zie je de 7 symmetrievlakken van een kubus.
Vuistregels
- Een symmetrievlak deelt een figuur in 2 gelijke delen die elkaars spiegelbeeld zijn.
Voorbeeldvraag
Geef het spiegelbeeld van
a. punt C
b. punt H
c. ribbe EH
Uitwerking:
a. Punt D is het spiegelbeeld van punt C. De lijn tussen CD staat loodrecht op de spiegel en punt C en D liggen beide even ver van de spiegel vandaan.
b. Punt G is het spiegelbeeld van punt H. De lijn tussen GH staat loodrecht op de spiegel en punt G en H liggen beide even ver van de spiegel vandaan.
c. Ribbe FG is het spiegelbeeld van ribbe EH.
