Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Basis - inhoud van een cilinder
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Basis - inhoud van een cilinder eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Basis - inhoud van een cilinder
Theorie
Uitdaging
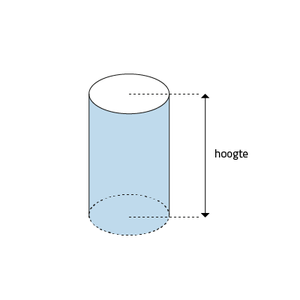
We kunnen de inhoud van verschillende ruimtelijke figuren berekenen. Zo'n figuur kan een cilinder zijn (zie afbeelding). Een cilinder heeft een cirkelvormig grondvlak en een bepaalde hoogte.
De inhoud van een cilinder is iets lastiger te berekenen dan die van een balk. Bij het berekenen van de inhoud gaat het bij beide vormen om hetzelfde principe: grondvlak vermenigvuldigen met de hoogte. In deze theorie leggen we uit hoe je de inhoud van een cilinder kunt berekenen.
Methode
Het grondvlak (en het bovenvlak) van een cilinder is een cirkel. De formule om de oppervlakte van een cirkel te berekenen is $$\pi · r^2$$.
Om de inhoud van een cilinder te berekenen moeten we de oppervlakte van deze cirkel (het grondvlak) vermenigvuldigen met de hoogte van de cilinder.
$$\mbox{Inhoud cilinder } = \pi · \mbox{straal}^2 \cdot \mbox{ hoogte}$$
De inhoud kan in verschillende eenheden gevraagd zijn. Onthoudt altijd goed dat 1 liter gelijk is aan 1 dm3 en dat dit weer gelijk is aan 1.000cm3.
1 liter = 1 dm3 = 1.000 cm3
Vuistregels
- Diameter = d
- Straal = r
- d = 2 · r
- Hoogte = h
- $$\mbox{Oppervlakte cirkel} = \pi · r^2$$
- $$\mbox{Inhoud cilinder} = \pi · r^2 · h$$
Voorbeeldvraag
Bereken de inhoud van een cilinder met een diameter van 14 cm en een hoogte van 45 cm in liter.
Uitwerking:
$$\mbox{Inhoud }= \pi · r^2 · \mbox{ hoogte}$$
$$r = \frac{1}{2} · 14 = 7 \mbox{ cm}$$
$$\mbox{Inhoud }= \pi · 7^2 · 45 \approx 6.927 \mbox{ cm}^3$$
1 liter = 1.000 cm3 ,dus $$\mbox{Inhoud} = \frac{6.927}{1.000} \approx 6,9 \mbox{ liter}$$
