Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Oppervlakte van een trapezium
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Oppervlakte van een trapezium eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Oppervlakte van een trapezium
Theorie
Uitdaging
Een trapezium is een vierhoek waarvan twee zijden evenwijdig zijn. Als de niet evenwijdige zijden even lang zijn heet zo'n trapezium een gelijkbenig trapezium. Een trapezium is dus ook een vierhoek, maarheeft slechts één paar evenwijdige zijdes.
In deze theorie bespreken we hoe we de oppervlakte van een trapezium kunnen berekenen.
Methode
Een trapezium bestaat uit vier hoeken en minimaal één paar evenwijdige lijnen. De oppervlakte van een trapezium kun je als volgt berekenen:
- $$\mbox{Oppervlakte trapezium}= \frac{1}{2} · \mbox{ som evenwijdige zijden} · \mbox{ bijbehorende hoogte}$$
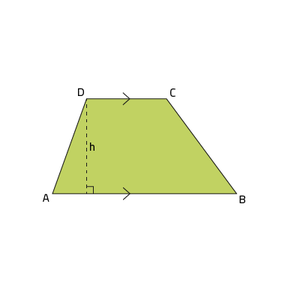
- Bijvoorbeeld in de afbeelding: $$\mbox{Oppervlakte } ABCD = \frac{1}{2} · (AB + CD) · h$$
Vuistregels
- $$\mbox{Oppervlakte trapezium}= \frac{1}{2} · \mbox{som evenwijdige zijden} · \mbox{ bijbehorende hoogte}$$
Voorbeeldvraag
Een parallellogram heeft een zijde van 9cm en een bijbehorende hoogte van 5cm, en is gevormd uit twee trapeziums. Bereken de oppervlakte van één trapezium.
Uitwerking
(a + b) = 9 cm
$$\mbox{Oppervlakte trapezium =} \frac{1}{2} · 9 · 5 = 22,5 \mbox{ cm}^2 $$
