Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Grafieken bij lineaire en kwadratische formules
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Grafieken bij lineaire en kwadratische formules eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Grafieken bij lineaire en kwadratische formules
Theorie
Uitdaging
Het is belangrijk om een lineaire en een kwadratische formule te kunnen onderscheiden en de grafiek ervan te kunnen schetsen.
In deze theorie leggen we je uit wat het verschil is tussen een lineaire en kwadratische formule en hoe je op basis van een formule een schets kunt maken van de grafieken van deze formules.
Methode
Lineaire formule
Een lineaire formule is een formule zoals y = x + 9. Om de grafiek hiervan te kunnen schetsen stel je eerst een tabel op:
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} x & -2 & -1 & 0 & 1 & 2 \T \\\hline y=x+9 \T & -2 + 9 =7 & -1+9=8 & 0+9=9 & 1+9=10 & 2+9=11 \end{array}$$
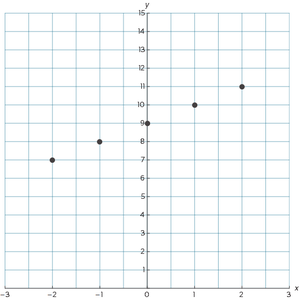
Je weet nu dat de volgende punten op de grafiek liggen: (-2,7), (-1,8), (0,9), (1,10) en (2,11).
- Teken deze punten op een figuur zoals in figuur 1.
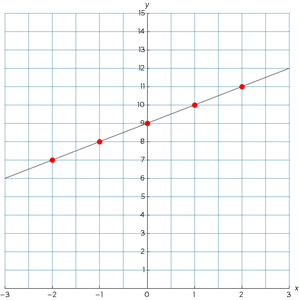
- Trek nu een lijn door de punten zoals in figuur 2.
Kwadratische formule
Een kwadratische formule is een formule zoals y = x2 + 9. Om de grafiek hiervan te kunnen schetsen stel je eerst een tabel op:
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} x & -2 & -1 & 0 & 1 & 2 \T \\\hline y=x^2+9 \T & (-2)^2 + 9 =13 & (-1)^2 +9=10 & (0)^2+9=9 & (1)^2+9=10 & (2)^2+9=13 \end{array}$$
Zoals je ziet geven, bijvoorbeeld, x = -2 en x = 2 dezelfde waarde voor y. Dit is omdat -2 en 2 allebei 4 zijn in het kwadraat: de regel is dat: (-x)2 = (x)2.
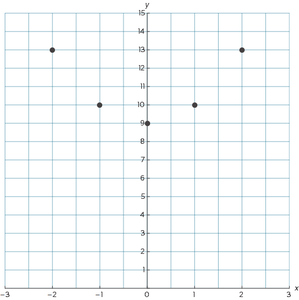
Je hoeft maar 1 van de 2 waardes uit te rekenen, de andere kun je daarna gewoon invullen in de tabel. Je weet nu dat de volgende punten op de grafiek liggen: (-2,13), (-1,10), (0,9), (1,10) en (2,13).
- Teken deze punten op een figuur zoals in figuur 3.
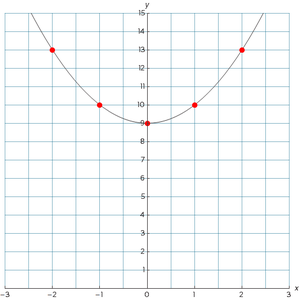
- Trek nu een vloeiende lijn door de punten zoals in figuur 4.
De grafiek van een kwadratische formule heet een parabool.
Vuistregels
- Lineaire formule: y = x + 9
- Kwadratische formule: y = x2 + 9
Voorbeeldvraag
Gegeven zijn de formules y = 2x2 + 7 en y = 2x + 7.
a. Vul de volgende tabellen in:
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} x & -2 & -1 & 0 & 1 & 2 \T \\\hline y=2x^2+7 \T&&&&& \end{array}$$
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} x & -2 & -1 & 0 & 1 & 2 \T \\\hline y=2x+7 \T&&&&& \end{array}$$
b. Schets beide grafieken op hetzelfde figuur. c. Welke formule is lineair en welke is kwadratisch?
Uitwerking
a. Vul de waarde van x in de formule om y te berekenen. Tabel 1:$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} x & -2 & -1 & 0 & 1 & 2 \T \\\hline y=2x^2+7 & 2(-2)^2+7& 2(-1)^2+7& 2(0)^2+7& 2(1)^2+7& 2(2)^2+7 \end{array}$$
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} x & -2 & -1 & 0 & 1 & 2 \T \\\hline y=2x^2+7 \T&15&9&7&9&15 \end{array}$$
Tabel 2:$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} x & -2 & -1 & 0 & 1 & 2 \T \\\hline y=2x+7 & 2(-2)+7& 2(-1)+7& 2(0)+7& 2(1)+7& 2(2)+7 \end{array}$$
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} x & -2 & -1 & 0 & 1 & 2 \T \\\hline y=2x+7 \T&3&5&7&9&11 \end{array}$$
b. De tabellen uit vraag a kunnen gebruikt worden om de grafieken te schetsen. Zie het figuur.
c. y = 2x2 + 7 is een kwadratische formule, de grafiek ervan is een vloeiende kromme genaamd een parabool (rood in de grafiek).y = 2x + 7 is een lineaire formule, de grafiek ervan is een rechte lijn (blauw in de grafiek).
