Slimleren.nl

Drie manieren om zijden en hoeken van driehoeken te berekenen

Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Drie manieren om zijden en hoeken van driehoeken te berekenen eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.

sinus
cosinus
tangens
Pythagoras
SOSCASTOA
verhoudingstabel
goniometrische verhoudingen
lijnen
lijnstukken
hoeken
driehoek

Theorie

Stelling van Pythagoras

Uitdaging

De stelling van Pythagoras, gelijkvormige driehoeken en goniometrische verhoudingen zijn verschillende manieren om lijnstukken te berekenen. Pythagoras en goniometrische verhoudingen kun je alleen toepassen op rechthoekige driehoeken.

Methode

Lijnstukken kun je berekenen op de volgende 3 manieren:

De stelling van Pythagoras

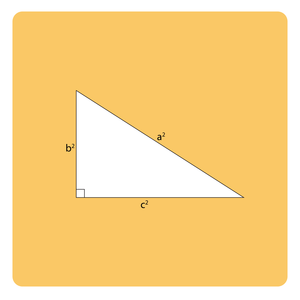
In het figuur: a² = b² + c²

Gelijkvormige driehoeken

Maak eerst een verhoudingstabel, daarna kun je kruislings vermenigvuldigen.

Goniometrische verhoudingen

Als je 2 van de 3 zijdes weet, kun je de hoeken in een rechthoekige driehoek uitrekenen.

Vuistregels

Stelling van Pythagoras: a² = b² + c²
Lijnstukken noteer je in alfabetische volgorde. Bijvoorbeeld AB i.p.v. BA.
SOSCASTOA

Voorbeeldvraag

Gegeven is de rechthoekige driehoek.

a. Bereken AC. b. Bereken ∠E.

Uitwerking:

a. Maak eerst een verhoudingstabel: $$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} AC & CE & AE \T \\\hline BC \T & CD & BD \end{array}$$

Vul de gegeven nummers in:$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} AC & CE & 7 \T \\\hline 8 \T & CD & 5\end{array}$$

Nu kun je kruiselings vermenigvuldigen om AC te vinden:$$AC=\frac{8·7}{5}=\frac{56}{5}=11,2$$

b. Om ∠E te vinden kun je goniometrische verhouding gebruiken omdat de driehoek rechthoekig is. Omdat we de aanliggende en overstaande zijdes weten kunnen we tangens gebruiken om de hoek uit te rekenen. $$\mbox{tan}(∠E)=\frac{11,2}{7}=1,6$$