Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Gelijkvormigheid in driehoeken
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Gelijkvormigheid in driehoeken eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Gelijkvormigheid in driehoeken
Theorie
Uitdaging
Als een figuur een vergroting, of verkleining is van een ander figuur, zijn deze gelijkvormig aan elkaar. Als twee figuren gelijkvormig zijn noteren we dat met een ~ teken.
Om gelijkvormig te zijn moeten figuren aan een aantal eisen voldoen. In deze theorie bespreken we gelijkvormigheid in driehoeken.
Methode
Twee figuren zijn gelijkvormig als het origineel en het vergrote/verkleinde figuur:
- Dezelfde vorm hebben
- Gelijke hoeken hebben
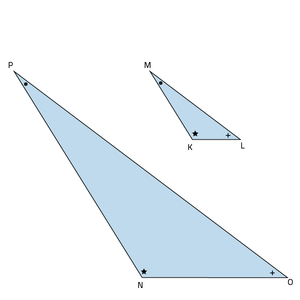
Aan de volgorde van de letters kun je zien welke hoeken overeenkomstige hoeken zijn. In de afbeelding zijn driehoek KLM en driehoek NOP weergegeven.
ΔKLM ~ ΔNOP
Aan de volgorde van de letters kan je opmaken dat:
∠K = ∠N
∠L = ∠O
∠M = ∠P
De zijden van gelijkvormige driehoeken passen altijd in een verhoudingstabel. Onbekende zijden kun je door middel van kruisproducten uitrekenen.
Bij deze driehoeken geeft dat de verhoudingstabel:
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} KL & LM & KM \T \\\hline NO \T & OP & NP \end{array}$$
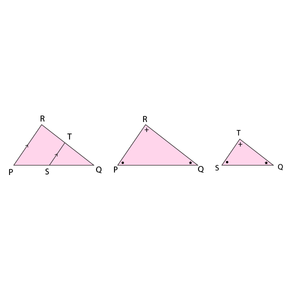
Twee driehoeken waarvan de ene in de ander zit, kunnen ook gelijkvormig zijn. In driehoek PQR kun je dit zien. Binnenin ΔPQR zit namelijk ΔSQT.
Deze driehoek zijn gelijkvormig als zijde PR evenwijdig is aan zijde ST. Want alleen dan zijn de hoeken van beide driehoeken gelijk aan elkaar en dat is een voorwaarde van gelijkvormigheid.
Vuistregels
- ~ is het teken voor gelijkvormigheid.
Voorbeeldvraag
a. Maak af ΔABC ~ Δ...
b. Bereken AC
c. Bereken EF
d. Maak af ΔKLM ~ Δ...
Uitwerking:
a. Zoek eerst de gelijke hoeken.
∠A = ∠D
∠B = ∠E
∠C = ∠F
Dus: ΔABC ~ ΔDEF
b. Maak eerst een verhoudingstabel van de driehoeken:
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} ΔABC & AB & BC & AC \T \\\hline ΔDEF \T & DE & EF & DF \end{array}$$
Vul nu de getallen in die gegeven zijn:
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} ΔABC & 3 & 7 & AC \T \\\hline ΔDEF \T & 9 & EF & 15 \end{array}$$
Splits de verhoudingstabel naar een tabel van 2x2 en zorg dat je maar 1 onbekend getal hebt, het getal waar je naar op zoek bent (AC in dit geval).
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} 3 & AC \T \\\hline 9 \T & 15 \end{array}$$
Nu kun je kruiselings vermenigvuldigen.
AC · 9 = 3 · 15
$$AC=\frac{3 · 15}{9}=\frac{45}{9}=5$$
c. Splits de originele tabel nogmaals met alleen EF als onbekend getal.
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} 3 & 7 \T \\\hline 9 \T & EF \end{array}$$
3 · EF = 9 · 7
$$EF=\frac{9 · 7}{3}=\frac{63}{3}=21$$
d. ΔKLM ~ ΔQLR
ΔKLM is niet gelijkvormig aan ΔNLP, omdat zijde NP niet evenwijdig is aan zijde KM. Hierdoor zijn niet alle hoeken gelijk aan elkaar en zijn de driehoeken dus niet gelijkvormig.
ΔQLR daarentegen is wel gelijkvormig aan ΔKLM. Zijde QR is namelijk evenwijdig aan zijde KM. Hierdoor geldt:
∠K = ∠Q
∠L = ∠L
∠M = ∠R
Dus: ΔKLM ~ ΔQLR
