Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Bijzondere kwadratische ongelijkheden
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Bijzondere kwadratische ongelijkheden eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Bijzondere kwadratische ongelijkheden
Theorie
Uitdaging
Een kwadratische ongelijkheid heeft de vorm van een kwadratische vergelijking, maar dan zijn de linker- en rechter kant van de vergelijking niet aan elkaar gelijk, maar juist ongelijk aan elkaar.
Ongelijkheden kunnen worden aangegeven met de tekens kleiner dan < en groter dan >. Hoe je deze vergelijkingen kunt oplossen leggen we je uit in deze theorie.
Methode
Kwadratische ongelijkheden kunnen verschillende grafieken tot stand brengen. Als (volgens de abc-formule) a > 0, dan is de grafiek een dalparabool en als a < 0, dan is de grafiek een bergparabool.
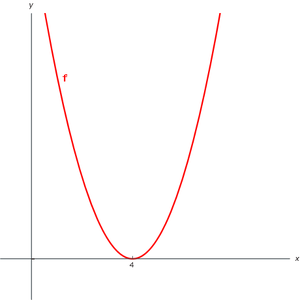
- Als we naar figuur 1 kijken, zien we dat f(x) groter dan 0 is behalve op x = 4. Dit noteren we als volgt: f(x) > 0 voor $$x {\neq} { 4} $$
Daarbij de f(x) voor geen enkele x kleiner dan 0, dus f(x) < 0 voor geen enkele x.
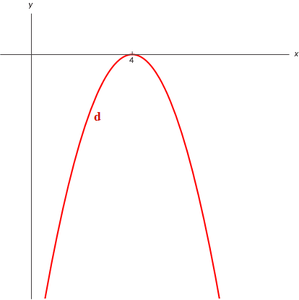
- Als we naar figuur 2 kijken, zien we dat voor d(x) het tegenovergestelde van f(x) geldt.
d(x) is voor geen enkele x groter dan 0, dus d(x) > 0 voor geen enkele x. Daarbij is d(x) voor alle x kleiner dan 0, behalve voor x = 4. Dus d(x) < 0 voor $$\mbox {x} {\neq} { 4} $$.
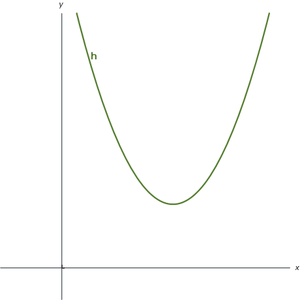
- In figuur 3 zien we dat h(x) voor alle x groter is dan 0 en voor geen enkele x kleiner is dan 0.
h(x) > 0 voor elke x
h(x) < 0 voor geen enkele x
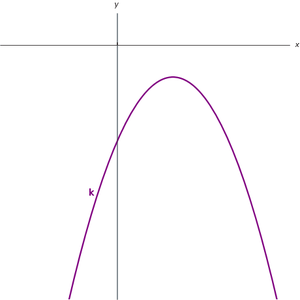
- In figuur 4 zien we dat k(x) voor alle x kleiner is dan 0 en voor geen enkele x groter is dan 0.
k(x) < 0 voor elke x
k(x) > 0 voor geen enkele x
Het oplossen van een bijzondere vergelijking kunnen we doen met de volgende stappen.
- Stap 1: Stel de vergelijking gelijk aan 0.
- Stap 2: Het aantal oplossingen voor een kwadratische ongelijkheid kunnen we bepalen door de discriminant te bepalen volgens de abc-formule.
- D > 0, er zijn 2 oplossingen.
- D = 0, er is 1 oplossing.
- D < 0, er zijn geen oplossingen.
- Stap 3: Bereken de oplossing.
- Stap 4: Kijk of de vergelijking een dal- of bergparabool is aan de hand van a en met de gevonden oplossingen kun je zien waar de grafiek de x-as snijdt.
- Stap 5: Nu kun je het antwoord noteren aan de hand van de vergelijking wanneer deze groter of kleiner dan 0 is.
Vuistregels
- D = b2 - 4 · a · c
- $$x=\frac{-b - \sqrt{D}}{2 · a} $$
- $$x=\frac{-b + \sqrt{D}}{2 · a} $$
- D > 0, er zijn 2 oplossingen.
- D = 0, er is 1 oplossing.
- D < 0, er zijn geen oplossingen.
- a > 0, dalparabool
- a < 0, bergparabool
- x2 = negatief, dan zijn er geen oplossingen.
Voorbeeldvraag
Los op.
a. x2 - 2x + 6 > 0
b. 2x2 + 3x - 4 < 0
Uitwerking
a. Stap 1: Stel de vergelijking gelijk aan 0.
x2 - 2x + 6 = 0
Stap 2: Indien zelf geen oplossing te vinden, gebruik abc-formule.
a = 1, b = -2, c = 6
D = -22 - 4 · 1 · 6 = -20
Stap 3: Bereken de oplossing.
D < 0, dus er zijn geen oplossingen.
Stap 4: Bepaal of de vergelijking een dal- of bergparabool is en kijk waar de grafiek de x-as snijdt.
De grafiek is een dalparabool, want a > 0, die de x-as niet snijdt.
b. Stap 1: Stel de vergelijking gelijk aan 0.
2x2 + 3x - 4 = 0
Stap 2: Indien zelf geen oplossing te vinden, gebruik abc-formule.
a = 2, b = 3, c = -4
D = 32 - 4 · 2 · -4 = 41
Stap 3: Bereken de oplossing.
D > 0, er zijn 2 oplossingen.
$$x=\frac{-3 - \sqrt{41}}{2 · 2} = -2,4$$
$$x=\frac{-3 + \sqrt{41}}{2 · 2} = 0,9$$
Stap 4: Bepaal of de vergelijking een dal- of bergparabool is en kijk waar de grafiek de x-as snijdt.
De grafiek is een dalparabool want a > 0 en snijdt de x-as in de punten (-2,4, 0) en (0,9, 0).
Stap 5: Noteer je antwoord voor wanneer de vergelijking kleiner is dan 0.
2x2 + 3x - 4 < 0 voor x < -2,4 en x > 0,9
