Welke lesstof is er beschikbaar in het programma van Slimleren?

Uitdaging

De sinus, cosinus en tangens zijn goniometrische verhoudingen. Dit klinkt ingewikkeld, maar dat valt best mee. Je kunt deze gebruiken om de hoeken en zijden te berekenen van rechthoekige driehoeken. Een rechthoekige driehoek is een driehoek met één rechte hoek (= 90°).

In deze theorie behandelen we alleen de sinus en leggen we uit hoe je hoeken kunt berekenen met behulp van de sinus.

Methode

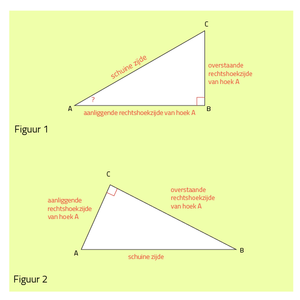
De sinus van een hoek geeft (net als de cosinus en de tangens) de verhouding aan tussen twee zijden van een rechthoekige driehoek. Eerder hebben we geleerd dat een rechthoekige driehoek altijd een schuine zijde heeft (die ligt tegenover de rechte hoek) en twee rechthoekszijden heeft (dit zijn de benen van de rechte hoek). De twee rechthoekszijden kun je ook beiden een eigen naam geven als je kijkt vanuit één bepaalde hoek: als je bijvoorbeeld naar Figuur 1 kijkt dan is zijde BC de overstaande rechthoekszijde van hoek A en zijde AB de aanliggende rechthoekszijde van hoek A. 

Een rekenregel die je goed moet onthouden is:

$$\bf{\text{sin}(\angle {A}) = \frac{\text{overstaande rechthoekszijde van } \angle A}{\text{schuine zijde}}}$$

Dit kun je goed onthouden door het woordje SOS (de eerste letters van de verschillende onderdelen: Sin, Overstaande, Schuine).

 

In figuur 1 zie je een driehoek met een (hellings)hoek A. De overstaande rechthoekszijde is BC en de schuine zijde is AC. De verhouding $$\frac{BC}{AC}$$ zegt dus iets over de hoek A. Deze verhouding heet de sinus van hoek A: $$\text{sin}(\angle{A}) = \frac{BC}{AC}$$.

Stel zijde BC is 3 en zijde AC is 5. Als je dit invult in de formule om hoek A te berekenen krijg je dus:$$\text{sin}(\angle{A}) = \frac{3}{5}$$. Nu weet je wat de sinus van hoek A is, maar je moet hoek A weten. Je moet daarvoor de inverse sinus gebruiken: op je rekenmachine zie je dit als $$\text{sin}^{-1}$$. Dit betekent dat $$\angle{A} = \mbox{sin}^{-1}\left(\frac{BC}{AC}\right)$$.

Als zijde BC 3 is en zijde AC 5 is, dan kom je dus uit op: $$\angle{A} = \mbox{sin}^{-1}\left(\frac{3}{5}\right) = 36,9°$$.

Let op dat je bij het berekenen van de verhouding, de juiste getallen door elkaar deelt. Omdat een driehoek ook kan draaien zit de rechte hoek niet altijd op dezelfde plek, zoals je kunt zien in figuur 2. Kijk dus goed welke zijde de schuine zijde, welke de aanliggende rechthoekszijde en welke de overstaande rechthoekszijde is.

 

Hoek berekenen

Als je weet hoelang de overstaande rechthoekszijde is en hoelang de schuine zijde is, kun je de hoek berekenen.

$$\bf{\angle A = \text{sin}^{-1} \left(\frac{\text{overstaande rechthoekszijde van }\angle A}{\text{schuine zijde}}\right)}$$

 

Zijden berekenen

Met behulp van de formule kun je ook een zijde berekenen als je de hoek weet.

$$\bf {\text{overstaande rechthoekszijde van } \angle A} = \text{sin}(\angle {A})·\mbox{schuine zijde}$$

$$\bf\text{schuine zijde}= \frac{\text{overstaande rechthoekszijde van } \angle{A}}{\text{sin}(\angle{A})}$$