Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Boxplot
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Boxplot eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Boxplot
Theorie
Uitdaging
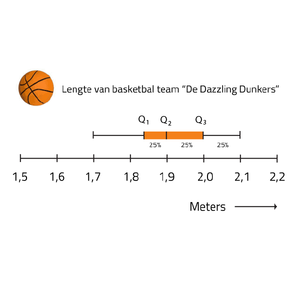
De spreidingsplot van de lengte van basketbalspelers wordt door de mediaan gedeeld in 2 helften. Het is nu alleen wel moeilijk om te zeggen hoe die helften verdeeld zijn. Het kan bijvoorbeeld zo zijn dat 50% van de spelers dichter richting de 1,70 m zitten dan 1,90. Of er is een kans dat maar 1 speler 1,70 is en de rest groter.
Om hier meer duidelijkheid over te krijgen, kan je een ook een boxplot maken. In deze theorie leggen we je uit wat een boxplot is en wat je ermee kunt.
Methode
Bij een boxplot worden nog twee medianen toegevoegd. De bovenste 50% en de onderste 50% worden ook in twee delen opgedeeld. Je krijgt dan 4 groepen die alle 4 bestaan uit (ongeveer) 25% van het aantal getallen in de waarnemingsreeks. De mediaan over de eerste helft (met de laagste getallen) heet het eerste kwartiel en wordt aangegeven met Q1. De mediaan over de tweede helft (met de hoogste getallen) heet het derde kwartiel en wordt aangegeven met Q3. Dit heet het derde kwartiel omdat driekwart van de getallen lager dan (of gelijk aan) dit getal zijn.
De medianen Q1 en Q3 bepaal je op dezelfde manier als Q2, maar dan neem je niet de volledige groep getallen maar alle getallen links van Q2 (om Q1 te bepalen) en alle getallen rechts van Q2 (om Q3 te bepalen). Als de waarnemingsreeks uit een oneven aantal bestaat wordt de mediaan zelf niet meegerekend bij een helft. De 2 helften zijn daarom altijd even groot. Als een helft uit een oneven aantal bestaat is het middelste getal het kwartiel. Als een helft uit een even aantal bestaat is het kwartiel het gemiddelde van de middelste 2 getallen. Let op: de mediaan (Q2) telt niet mee.
Vuistregels
- Een boxplot geeft een verdeling in 4 delen van 25%.
Voorbeeldvraag
Van alle leraren klassieke talen bij een middelbare scholengemeenschap wordt de leeftijd genoteerd in een tabel.
$$\newcommand\Docent{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} \mbox{Docent} & \mbox{Tina} & \mbox{Mirjam} & \mbox{Henk} & \mbox{Guusje} & \mbox{Theo} & \mbox{Robert-Paul} & \mbox{Dieni} & \mbox{Helen} & \mbox{Sandrien} \\\hline \mbox{Leeftijd} & 35 & 41 & 45 & 48 & 50 & 51 & 52 & 58 & 60 \end{array}$$
a. Wat is de mediaan?
b. Ervan uitgaande dat de mediaan niet mee doet, welke leraren vallen er dan in de jongste 25%? En in de oudste 25%?
c. Teken een boxplot voor deze verdeling.
Uitwerking
a. Het middelste getal van de reeks van 9 leraren, is de 5e docent. Dit is hier dus de mediaan. Hier is dat Theo en die is 50. De mediaan ligt dus bij 50.
b. In totaal zijn het 9 leraren, de 5e docent is de mediaan. Aan weerszijden van de mediaan zijn nog 4 docenten, elke 4 vormen 50%. De helft van die 50% is 2 docenten. Dus de jongste 25% zijn de 2 jongste leraren: Tina en Mirjam. Hetzelfde geldt voor de oudste 25%. Dit zijn de 2 oudste leraren: Helen en Sandrien.
c. Bepaal Q1 en Q3: $$Q1=\frac{41+45}{2}=43$$ en $$Q3=\frac{52+58}{2}=55$$. Verwerk deze waarden in een boxplot. Zie de afbeelding "Leraren".
