Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Hoeken berekenen met de sinus, cosinus en tangens
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Hoeken berekenen met de sinus, cosinus en tangens eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Hoeken berekenen met de sinus, cosinus en tangens
Theorie
Uitdaging
Sinus, cosinus en tangens worden goniometrische verhoudingen genoemd. Je kan in een rechthoekige driehoek van elke scherpe hoek de sinus, cosinus en tangens als de verhouding van zijden opschrijven.
In deze theorie leggen we je de basis uit van hoe je met de sinus, cosinus en tangens kunt werken om zo elke scherpe hoek van een rechthoekige driehoek te kunnen berekenen.
Methode
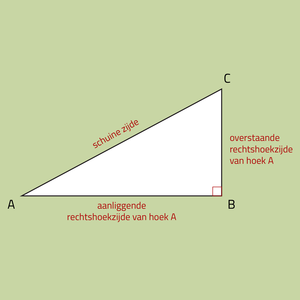
De sinus, cosinus en tangens geven allen de verhouding aan tussen twee zijden van een rechthoekige driehoek. Eerder hebben we geleerd dat een rechthoekige driehoek altijd een schuine zijde heeft (die ligt tegenover de rechte hoek) en twee rechthoekszijden heeft (dit zijn de benen van de rechte hoek). De twee rechthoekszijden kun je ook beiden een eigen naam geven als je kijkt vanuit één bepaalde hoek: als je bijvoorbeeld naar de afbeelding kijkt dan is zijde BC de overstaande rechthoekszijde van hoek A en zijde AB de aanliggende rechthoekszijde van hoek A.
De volgende formules zijn daarbij belangrijk om te onthouden:
Sinus: $$\bf\mbox{sin }(\angle{A}) = \frac{\mbox{ overstaande rechtshoekzijde van} { \angle{A}}}{\mbox{ schuine zijde}} = \frac{\mbox{BC}}{\mbox{AC}}$$
Cosinus: $$\bf\mbox{cos }(\angle{A}) = \frac{\mbox{ aanliggende rechtshoekzijde van} { \angle{A}}}{\mbox{ schuine zijde}} = \frac{\mbox{AB}}{\mbox{AC}}$$
Tangens: $$\bf\mbox{tan }(\angle{A}) = \frac{\mbox{ overstaande rechtshoekzijde van} { \angle{A}}}{\mbox{ aanliggende rechtshoekzijde van} { \angle{A}}} = \frac{\mbox{BC}}{\mbox{AB}}$$
Hoe je met de sinus, cosinus en tangens rekent, kun je onthouden met het woord: SOSCASTOA.
- SOS: Sinus is de Overstaande rechthoekszijde gedeeld door de Schuine zijde
- CAS: Cosinus is de Aanliggende rechthoekszijde gedeeld door de Schuine zijde.
- TOA: Tangens is de Overstaande rechthoekszijde gedeeld door de Aanliggende rechthoekszijde.
De laatste belangrijke stap is om het aantal graden van de hoek uit te rekenen. Stel AB = 7 en AC = 9. Dan weet je dat $$\bf\mbox{cos }(\angle{A}) = \frac{\mbox{ aanliggende rechtshoekzijde van} { \angle{A}}}{\mbox{ schuine zijde}} = \frac{\mbox{7}}{\mbox{9}}$$ dus $$\bf\mbox{cos }(\angle{A}) = \frac{\mbox{7}}{\mbox{9}}$$
Om nu te bepalen hoeveel graden hoek A is, oftewel wat de waarde is van $$\angle{A}$$ moet je de omgekeerde cosinus op je rekenmachine gebruiken (ook wel de inverse cosinus genoemd). Je kunt hiervoor op je rekenmachine de knoppen SHIFT+cos gebruiken, je ziet dat er dan cos-1 komt te staan.
Je krijgt dan $$\angle A=\mbox{cos}^{-1}\left(\frac{\mbox{aanliggende zijde van }\angle A}{\mbox{schuine zijde}}\right) = \mbox{cos}^{-1}\left(\frac{\mbox{7}}{\mbox{9}}\right) \approx 39°$$
Vuistregels
- $$\mbox{Sin }(\angle {A}) = \frac{\mbox{ overstaande rechthoekszijde van} \angle{A}}{\mbox{ schuine zijde}}$$
- $$\mbox{Cos }(\angle{A}) = \frac{\mbox{ aanliggende rechthoekszijde van}\angle{A}}{\mbox{ schuine zijde}}$$
- $$\mbox{Tan }(\angle{A}) = \frac{\mbox{ overstaande rechthoekszijde van} \angle{A}}{\mbox{ aanliggende rechthoekszijde van}\angle{A}}$$
Voorbeeldvraag
Gegeven is $$\Delta{MNO}$$ met $$\angle{O = 90°}$$ zoals in de afbeelding.
Schrijf als verhouding van 2 zijden.
a. $$\mbox{Sin }(\angle{N})$$
b. $$\mbox{Tan }(\angle{N})$$
c. $$\mbox{Sin }(\angle{M})$$
d. $$\mbox{Cos }(\angle{M})$$
Uitwerking:
a. $$\mbox{Sin }(\angle{N}) = \frac{\mbox{ overstaande rechthoekszijde van}\angle{N}}{\mbox{ schuine zijde}} = \frac{MO}{MN}$$
b. $$\mbox{Tan }(\angle{N}) =\frac{\mbox{ overstaande rechthoekszijde van}\angle{N}}{\mbox{ aanliggende rechthoekszijde van}\angle{A}} = \frac{MO}{NO}$$
c. $$\mbox{Sin }(\angle{M}) = \frac{\mbox{ overstaande rechthoekszijde van}\angle{M}}{\mbox{ schuine zijde}} = \frac{NO}{MN}$$
d. $$\mbox{Cos } (\angle{M}) = \frac{\mbox{ aanliggende rechthoekszijde van}\angle{M}}{\mbox{ schuine zijde}} = \frac{MO}{MN}$$
