Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Basis - de discriminant en het aantal snijpunten van de x-as met de parabool
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Basis - de discriminant en het aantal snijpunten van de x-as met de parabool eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Basis - de discriminant en het aantal snijpunten van de x-as met de parabool
Theorie
Uitdaging
De discriminant van een kwadratische vergelijking bereken je met de formule D = b2 - 4ac. De discriminant kan een negatief getal zijn, een positief getal zijn of gelijk zijn aan nul.
De discriminant is bepalend in het aantal oplossing van de kwadratische vergelijking. Ook kun je met behulp van de discriminant conclusies maken over de positie van de parabool die bij de kwadratische vergelijking hoort.
Hoe dit precies werkt oefen je hier.
Methode
De discriminant bereken je met de formule D = b2 - 4ac.
Als:
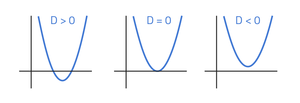
D > 0, dan zijn er 2 oplossingen voor de vergelijking. Dit betekent dat er 2 snijpunten met de x-as zijn.
D = 0, dan is er 1 oplossing voor de vergelijking. Dit betekent dat er 1 punt is waarbij de parabool de x-as raakt.
D < 0, dan zijn er geen oplossingen voor de vergelijking. Dit betekent dat de parabool de x-as nooit snijdt.
In de afbeelding kun je zien hoe de verschillende parabolen er uit zien.
Vuistregels
- D > 0, dan zijn er 2 oplossingen voor de vergelijking. Dit betekent dat er 2 snijpunten met de x-as zijn.
- D = 0, dan is er 1 oplossing voor de vergelijking. Dit betekent dat er 1 punt is waarbij de parabool de x-as raakt.
- D < 0, dan zijn er geen oplossingen voor de vergelijking. Dit betekent dat de parabool de x-as nooit snijdt.
Voorbeeldvraag
Hoeveel snijpunten met de x-as heeft deze parabool.
y = 3x2 + 2x + 3
Uitwerking
a = 3
b = 2
c = 3
$$D = b^2 - 4ac = 2^2 - 4 · 3 · 3 = 4 - 36 = -32$$
D < 0, dus geen snijpunten met de x-as.
