Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Gevorderd - zijden berekenen met de tangens
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Gevorderd - zijden berekenen met de tangens eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Gevorderd - zijden berekenen met de tangens
Theorie
Uitdaging
We hebben geleerd dat je met behulp van de tangens een hoek in een rechthoekige driehoek kunt berekenen als je de lengte van de overstaande en de aanliggende zijde van die hoek weet.
Andersom kun je ook met behulp van een hoek en een zijde de lengte van een andere zijde berekenen. In deze theorie leggen we je uit hoe dat precies werkt.
Methode
De formule die we kennen om met behulp van de tangens een hoek te berekenen, is als volgt:
$$\bf{\text{tan} (\angle A) = \frac{\text{overstaande rechthoekszijde van }\angle A}{\text{aanliggende rechthoekszijde van }\angle A}}$$
Als je nu deze formule omschrijft zodat een van de zijden alleen aan de linkerkant staat, dan kun je zien hoe je deze zijde kunt berekenen als de andere gegevens (de hoek en de andere zijde) bekend zijn:
$$\bf {\text{overstaande rechthoekszijde van } \angle A} = \text{tan}(\angle {A})·\mbox{aanliggende rechthoekszijde van }\angle A$$
$$\bf\text{aanliggende rechthoekszijde van }\angle A = \frac{\text{overstaande rechthoekszijde van } \angle{A}}{\text{tan}(\angle{A})}$$
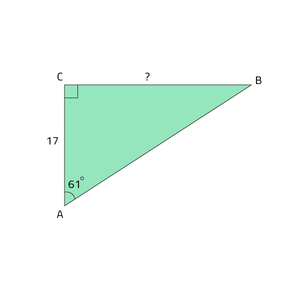
Dus als een hoek met de aanliggende rechthoekszijde is gegeven dan kun je de overstaande rechthoekszijde berekenen. Bijvoorbeeld in afbeelding Driehoek 1. $$\mbox{tan}(\angle A) = \frac{BC}{AC}$$ dus $$\mbox{tan}(61) = \frac{BC}{17}$$
Je kunt nu de onbekende variabele BC (= de overstaande zijde) naar de linkerkant halen (zie ook hierboven de al omgeschreven formule waarbij de overstaande rechthoekszijde al aan de linkerkant staat):
$$\text{overstaande rechthoekszijde van } \angle A = BC = \text{tan}(61)·\mbox{17 }\approx 30,7$$
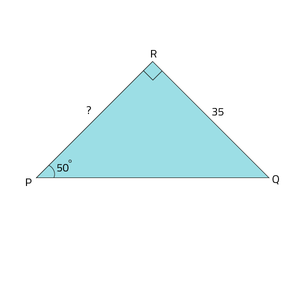
Als een hoek met de overstaande rechthoekszijde is gegeven dan kun je de aanliggende rechthoekszijde berekenen. Bijvoorbeeld in afbeelding Driehoek 2. $$\mbox{tan}(\angle P) = \frac{QR}{PR}$$ dus $$\mbox{tan}(50) = \frac{35}{PR}$$
Je kunt nu de onbekende variabele PR (= de aanliggende zijde) naar de linkerkant halen (zie ook hierboven de al omgeschreven formule waarbij de aanliggende rechthoekszijde al aan de linkerkant staat):
$$\text{aanliggende rechthoekszijde van } \angle P = PR = \frac{\text{35}}{\text{tan}(50)} \approx 29,4$$
Vuistregels
-
$$\bf {\text{overstaande rechthoekszijde van } \angle A} = \text{tan}(\angle {A})·\mbox{aanliggende rechthoekszijde van }\angle A$$
-
$$\bf\text{aanliggende rechthoekszijde van }\angle A = \frac{\text{overstaande rechthoekszijde van } \angle{A}}{\text{tan}(\angle{A})}$$
Voorbeeldvraag
De aanliggende rechthoekszijde van $$\angle A$$ is gegeven. Bereken de overstaande rechthoekszijde van $$\angle A$$ in 1 decimaal nauwkeurig.
Uitwerking:
$$\mbox{tan}(\angle A) = \frac{BC}{AC}$$ dus $$\mbox{tan}(42) = \frac{BC}{12}$$
Je kunt nu de onbekende variabele BC (= de overstaande zijde) naar de linkerkant halen (zie ook hierboven de al omgeschreven formule waarbij de overstaande rechthoekszijde al aan de linkerkant staat):
$$\text{overstaande rechthoekszijde van } \angle A = BC = \text{tan}(42)·\mbox{12 }\approx 10,8$$
