Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Exponentiële groei in een reeks vinden
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Exponentiële groei in een reeks vinden eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Exponentiële groei in een reeks vinden
Theorie
Uitdaging
Bij exponentiële groei wordt een hoeveelheid steeds met hetzelfde getal vermenigvuldigd.
In deze theorie leggen we je uit hoe je kunt uitvogelen of een reeks exponentieel groeit.
Methode
Om na te gaan of een reeks exponentieel groeit, kun je het volgende doen:
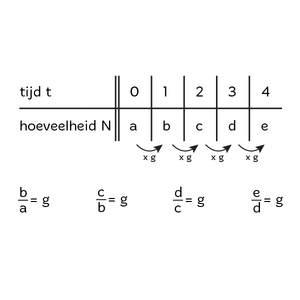
Stap 1: Deel een bepaalde hoeveelheid door de vorige hoeveelheid.
In de afbeelding: $$\frac{b}{a}=g$$
Stap 2: Doe dit voor een aantal getallen in de reeks. In de afbeelding: $$\frac{c}{b}=g$$ en $$\frac{d}{c}=g$$ en $$\frac{e}{d}=g$$
Stap 3: Wanneer er steeds hetzelfde getal uitkomt (de groeifactor g), dan kun je aannemen dat de reeks exponentieel groeit.
Vuistregels
- Deel een bepaalde hoeveelheid door de vorige hoeveelheid.
- Doe dit voor een aantal getallen in de reeks.
- Wanneer er ongeveer hetzelfde getal uitkomt (de groeifactor g), kun je aannemen dat de reeks exponentieel groeit.
Voorbeeldvraag
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} \mbox{Tijd in jaren }t & 0 & 1 & 2 & 3 & 4 \T \\\hline \mbox{Hoeveelheid }N & 136 & 177 & 230 & 299 & 388 \end{array}$$
a. Is er in dit voorbeeld sprake van exponentiële groei? Zo ja, bereken de groeifactor
b. Hoe ziet de exponentiële formule van deze tabel eruit?
Uitwerking
a. $$\frac{177}{136}≈1,3$$, $$\frac{230}{177}≈1,3$$, $$\frac{299}{230}=1,3$$ en $$\frac{388}{299}≈1,3$$.
Alle delingen zijn ongeveer 1,3, dus er kan uitgegaan worden van exponentiële groei en de groeifactor is 1,3.
b. De beginhoeveelheid is 136, de formule om de hoeveelheid te berekenen wordt dus: $$N = 136 · 1,3^t$$.
