Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Gecombineerde snavel- en zandloperfiguren
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Gecombineerde snavel- en zandloperfiguren eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Gecombineerde snavel- en zandloperfiguren
Theorie
Uitdaging
In sommige figuren zitten zowel snavelfiguren als zandloperfiguren. Dit is het geval als er parallellogrammen en/of rechthoeken voorkomen in het figuur.
Het is dan van belang te denken aan de eigenschappen van deze figuren om de gevraagde zijde alsnog te kunnen berekenen. In deze theorie bespreken we gecombineerde snavel- en zandloperfiguren.
Methode
Een belangrijke eigenschap van parallellogrammen en rechthoeken is dat de overstaande zijden altijd gelijk zijn aan elkaar. Deze eigenschap zal je soms nodig hebben om de lengte van een zijde te vinden.
Het kan voorkomen dat een lijnstuk gevraagd wordt dat niet direct met kruisproducten op te lossen is. Geef het onbekende lijnstuk dan een naam in de kruistabel, zoals de naam van de zijde, of bijvoorbeeld 'x'. Je kan dan een vergelijking opstellen om de lengte van de gevraagde zijde alsnog te bepalen.
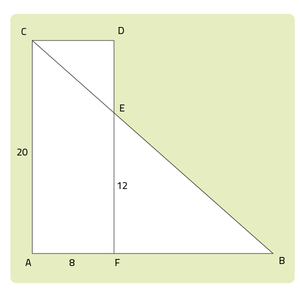
Bijvoorbeeld in figuur 1. In deze figuur zit een snavelfiguur en een zandloperfiguur. Het zandloperfiguur kun je niet gebruiken, omdat je maar 1 zijde kent van dit figuur. Het snavelfiguur kun je wel gebruiken.
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} AC & AB \T \\\hline \ EF & BF\end{array}$$
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} 20 & 8 + BF \T \\\hline \ 12 & BF\end{array}$$
(8 + BF) · 12 = 20 · BF
96 + 12BF = 20BF
96 = 8BF $$BF = \frac{96}{8} = 12$$
Ook kan het voorkomen dat je een deel van een lijnstuk uit moet rekenen om een overstaand lijnstuk te vinden. Vergeet hierbij ook niet de eigenschappen van een parallellogram en rechthoeken.
Om een zijde in een figuur te vinden moet je dus stap voor stap te werk gaan. Soms kun je de gevraagde zijde in 1 stap berekenen, soms moet je eerst andere zijden berekenen voordat je de gevraagde zijde kunt vinden.
Vuistregels
- Overstaande zijden in parallellogrammen/rechthoeken/vierkanten zijn gelijk aan elkaar.
Voorbeeldvraag
a. Bekijk figuur 1. Bereken de lengte van lijnstuk AE.
b. Bekijk figuur 2. Bereken de lengte van lijnstuk AC.
Uitwerking:
a. Stel eerst de kruistabel op en vul deze zoveel mogelijk in.
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} AC & BC \T \\\hline AE & EF \end{array} = \newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} AE+5 & 15 \T \\\hline AE & 8 \end{array}$$
Los het kruisproduct op door het op te lossen als een ongelijkheid.
(5 + AE) · 8 = 15 · AE
40 + 8 · AE = 15 · AE
7 ·AE = 40
$$AE \approx 5,7$$
b. Je kunt deze zijde berekenen door eerst de zijde DE te berekenen. DE + EF = DF. DF is een onderdeel van de parallellogram ADFC, Hierin zijn de zijde DF en AC hetzelfde. Zo vind je dus de zijde AC.
Om DE te bepalen gebruik je de methode van de zandloperfiguren. Zo kan je een kruisproduct opstellen:
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} EF & CE \T \\\hline \ DE & BE \end{array}$$
Je kan nu dus de zijde DE bepalen door de waarden van de andere zijden in de kruistabel in te vullen. $$DE = \frac{EF · BE}{CE} = \frac{ 4 · 6}{10} = 2,4$$
AC = 2,4 + 4 = 6,4
Een andere manier kan zijn dat je eerst zijde DE bepaalt met behulp van het zandloperfiguur en vervolgens zijde AC bepaalt met behulp van het snavelfiguur.
