Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Machten delen
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Machten delen eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Machten delen
Theorie
Uitdaging
Het kan zijn dat een macht onderdeel is van een breuk. Zulke breuken kunnen we ook herleiden. Hiervoor moet je de rekenregels kennen.
Hoe je sommen met machten die door elkaar worden gedeeld kunt herleiden leer je in deze theorie.
Methode
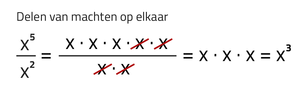
Er zijn twee belangrijke regels bij het delen van machten:
- Het grondtal van de machten, in dit geval x, moet hetzelfde zijn.
$$\frac{x^a}{x^b}=x^{a - b}$$
- De exponenten trek je van elkaar af. Bijvoorbeeld:
$$\frac{x^6}{x^2}=x^4$$ , want 6 - 2 = 4.
Daarnaast geldt:
$$\frac{6x}{6x} = 1 $$ $$\frac{x^4}{x^4}=1$$
Vuistregels
- $$\frac{x^a}{x^b} = x^{a - b}$$
Voorbeeldvraag
Herleid.
$$\frac{9a^{10}}{3a^5}$$
Uitwerking
Het grondtal is gelijk, dus trek je de exponenten van elkaar af, 10 - 5 = 5. De rest van de breuk gaat hetzelfde als een normale breuk, dus $$\frac{9}{3}=3$$.
Antwoord = 3a5
