Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Gevorderd - coördinaten op een lineaire grafiek
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Gevorderd - coördinaten op een lineaire grafiek eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Gevorderd - coördinaten op een lineaire grafiek
Video
Theorie
Uitdaging
Als er een coördinaat en een lineaire formule gegeven is, dan kun je checken of dit coördinaat op de lineaire formule ligt.
Hoe je met coördinaten en lineaire formules kunt rekenen leggen we je uit in deze theorie.
Methode
Coördinaat invullen in de functie
Je kunt direct het gegeven coördinaat invullen in de functie om erachter te komen of het coördinaat op de functie ligt. Je vult de x-coördinaat op de plek van de x in in de formule, en de y-coördinaat op de plek van de y in in de formule.
Tabel maken
Je kunt ook eerst een tabel maken en daarna checken of het coördinaat in de tabel voorkomt.
$$ \newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} x & -1 & 0 & 1 & 2 & 3 \T \\\hline f(x) & 1 & 2 & 3 & 4 & 5 \end{array} $$
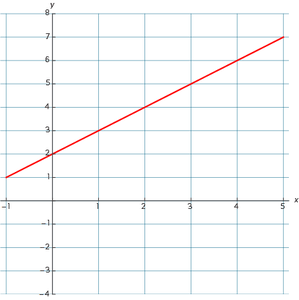
Dit is de tabel bij de functie f(x) = x + 2. Je kan nu de coördinaten aflezen uit de tabel en een grafiek tekenen bij de functie.
In de tabel van de functie kun je dus punten aflezen. Neem punt A(-1,1).
f(-1) = 1, dus het punt (-1,1) ligt op de grafiek van f.
Punt A(-1,1) heeft dus de x en y coördinaten XA = -1 en YA = 1.
Vuistregels
- De algemene vorm van een lineaire functie is f(x) = ax + b
- Door het gegeven coördinaat in te vullen in de functie kun je erachter komen of het coördinaat op de functie ligt
Voorbeeldvraag
Gegeven is de functie f(x) = 4x + 1.
a. Teken de grafiek van f(x).
b. Onderzoek of het punt P(6,20) op de grafiek van f ligt.
c. De y-coördinaat van punt A op de grafiek van f is yA= -7 . Bereken de x-coördinaat xA.
Uitwerking
a. Maak eerst een tabel.
$$ \newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} x & -1 & 0 & 1 & 2 & 3 \T \\\hline y & -3 & 1 & 5 & 9 & 13 \end{array} $$
Zie de grafiek in de afbeelding.
b. Om te onderzoeken of punt P(6, 20) op de grafiek van f ligt vul je de xP in in de formule.
f(6) = 4 · 6 + 1 = 25
Punt P(6, 20) ligt dus niet op de grafiek van f.
c. yA= -7 betekent dat f(x) = -7
f(x) = -7
4x + 1 = -7
4x = -8
x = -2
Dus xB= -2
