Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Kruisproducten en de verhoudingstabel
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Kruisproducten en de verhoudingstabel eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Kruisproducten en de verhoudingstabel
Video
Theorie
Uitdaging
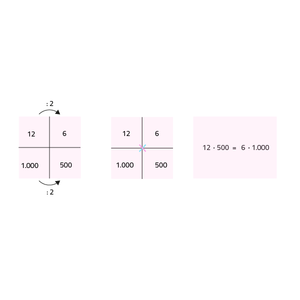
Als je pannenkoeken wilt bakken, maar niet een heel pak op wilt eten, dan moet je een beetje rekenen voordat je kunt gaan bakken. Hiervoor kun je een verhoudingstabel gebruiken. Stel dat je met 1 pak 12 pannenkoeken kunt bakken. En stel dat je hiervoor 1.000 milliliter melk nodig hebt.
Als je maar 6 pannenkoeken wilt bakken, dan heb je nog maar 500 milliliter melk nodig. Dit kun je in een verhoudingstabel zetten.
Bij berekeningen met verhoudingstabellen kun je kruisproducten gebruiken. In een verhoudingstabel zijn kruisproducten gelijk aan elkaar.
Methode
Een kruisproduct is een product van kruislings vermenigvuldigen. Kijk nog even naar de verhoudingstabel van de pannenkoeken:
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} 12 & 6 \T \\\hline 1.000 \T & 500 \end{array}$$
De producten 12 · 500 en 6 · 1.000 zijn gelijk aan elkaar. Deze producten noemen we kruisproducten.
Kruisproducten kunnen we ook algemeen formuleren:$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} a & c \T \\\hline b & d \end{array}$$
De kruisproducten zijn hier: a · d en b · c.
Kruisproducten in een verhoudingstabel staan gelijk aan elkaar dus ad = bc
Stel dat je bij deze verhoudingstabel wilt berekenen wat x is.
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} 3 & 9 \T \\\hline x & 15 \end{array}$$
3 · 15 = x · 9
$$x = \frac{3 · 15}{9} = 5$$
Ook in een langere verhoudingstabel zijn de kruisproducten gelijk, zoals deze verhoudingstabel:
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} 2 & 12 & 14 \T \\\hline 3 & 18 & 21 \end{array}$$
Je kunt de tabel telkens splitsen in een kleinere tabel met 2 kolommen en vervolgens de kruisproducten berekenen
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} 2 & 12 \T \\\hline 3 & 18 \end{array}$$ --> 2 · 18 = 3 · 12 $$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} 2 & 14 \T \\\hline 3 & 21\end{array}$$ --> 2 · 21 = 3 · 14 $$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} 12 & 14 \T \\\hline 18 & 21 \end{array}$$ --> 12 · 21 = 14 · 18
Vuistregels
- In een verhoudingstabel zijn kruisproducten gelijk aan elkaar.
Voorbeeldvraag
Gegeven is de verhoudingstabel $$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} 4 & x &16 \T \\\hline 12 & 6 & y\end{array}$$.
a. Bereken x
b. Bereken y
Uitwerking
a. $$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} 4 & x \T \\\hline 12 & 6\end{array}$$
4 · 6 = x · 12
$$x = \frac{4 · 6}{12} = 2$$
b. $$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} 4 & 16 \T \\\hline 12 & y\end{array}$$
4 · y = 16 · 12
$$y = \frac{16 · 12}{4} = 48$$
