Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Basis - evenwijdige lijnen
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Basis - evenwijdige lijnen eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Basis - evenwijdige lijnen
Theorie
Uitdaging
Lijnen van lineaire functies hebben de overeenkomst dat het rechte lijnen zijn, zonder bochten of hoeken erin. Het komt weleens voor dat de lijnen van verschillende functies even stijl zijn.
Hoe dit heet en hoe je dit kunt herkennen, leggen we je uit in deze theorie.
Methode
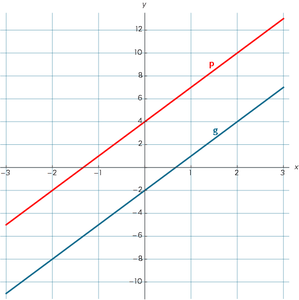
Bekijk de afbeelding. Lijn p en lijn g lopen precies in dezelfde richting oftewel precies even steil. We noemen dit evenwijdige lijnen. Als twee lijnen evenwijdig aan elkaar zijn, betekent dit dat de richtingscoëfficiënten (a) van beide lijnen aan elkaar gelijk zijn.
Lijnen p: y = 3x + 4 en g: y = 3x - 2 hebben dezelfde richtingscoëfficiënt, namelijk: rcp = rcg = 3 en zijn dus evenwijdig aan elkaar.
Je kunt dus evenwijdige lijnen herkennen door naar de richtingscoëfficiënt (oftewel de a) van de formule te kijken.
Als punt R(x,y) op de lijn ligt en je weet de richtingscoëfficiënt dan kan je b berekenen door de coördinaten van het punt in de formule in te vullen. Andersom geldt ook dat als je de formule weet, je kunt nagaan of een punt op de lijn ligt.
Vuistregels
- $$\mbox{Richtingscoëfficiënt} (a) = \frac{\mbox{verticale afstand}}{\mbox{horizontale afstand}}$$.
- Twee lineaire grafieken met dezelfde richtinscoëfficieënt zijn evenwijdig aan elkaar
- Twee evenwijdige lineaire lijnen hebben dezelfde richtingscoëfficiënt
Voorbeeldvraag
Lijn k met formule y = ax + b is evenwijdig aan lijn m met de formule m: y = 2x + 5 en lijn k gaat door het punt (4,5).
Geef de volledige formule van lijn k.
Uitwerking
De lijnen k en m zijn evenwijdig aan elkaar, wat betekent dat zij dezelfde richtingscoëfficiënt hebben.
Voor lijn k geldt dus ook a = 2.
Voor het berekenen van b vul je het punt (4,5), dat op lijn k ligt, in de formule y = 2x + b in.
De x-coördinaat is 4 en die vul je in voor x.
De y-coördinaat is 5 en die vul je in voor y.
5 = 2 · 4 + b
5 = 8 + b
-3 = b
De volledige formule voor lijn k: y = 2x - 3.
