Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Ontbinden in factoren op twee manieren
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Ontbinden in factoren op twee manieren eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Ontbinden in factoren op twee manieren
Video
Theorie
Uitdaging
Kwadratische vergelijkingen hebben de vorm ax2 +bx +c = 0. Kwadratische vergelijkingen kun je ontbinden in factoren. Dit kan op verschillende manieren. Om vragen over ontbinden in factoren goed te beantwoorden, moet je dus deze verschillende manieren goed onder de knie krijgen!
Methode
Manier 1: De gemeenschappelijke factor buiten haakjes halen
- x2 + 3x = 0 --> Gemeenschappelijke factor = x --> x(x + 3) = 0
- 16x2 - 4x = 0 --> Gemeenschappelijke factor = 4x --> 4x(4x - 1) = 0
Manier 2: De product-som-methode
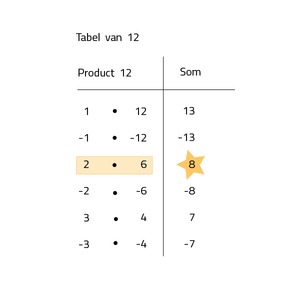
Bij de product-som-methode zoek je twee getallen waarvan de som b is en het product c. Je kan hierbij voor jezelf een tabel maken om de getallen te vinden, hiervan is een voorbeeld gegeven.
- x2 + 8x + 12 = 0 --> (x + 2)(x + 6) = 0 (zie afbeelding 'Tabel van 12')
- x2 - x - 72 = 0 --> (x - 9)(x + 8) = 0
Vuistregels
Ontbinden in factoren methoden:
- Gemeenschappelijke factor buiten haakjes halen
- Product-som-methode
Voorbeeldvraag
Ontbind de volgende sommen in factoren:
a. 8x2 + 4x
b. x2 + 14x + 40
Uitwerking
a. 8x2+ 4x
Haal de gemeenschappelijke factor buiten de haakjes.
4x(2x + 1)
b. x2 + 14x + 40
Gebruik de product-som-methode. Het product moet 40 zijn en de som 14. De getallen die je zoekt zijn 10 en 4.
(x + 10)(x + 4)
