Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Snijpunten van een kwadratische en lineaire formule
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Snijpunten van een kwadratische en lineaire formule eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Snijpunten van een kwadratische en lineaire formule
Video
Theorie
Uitdaging
De snijpunten van een lineaire en een kwadratische formule zijn de punten in de grafiek waar deze twee lijnen elkaar snijden. De coördinaten van deze punten, dus de waarde van de x-as en de y-as van deze punten, kun je berekenen.
In deze theorie leggen we je uit hoe dit precies werkt.
Methode
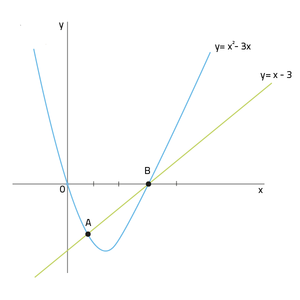
Stel je hebt grafieken van de formules y = x2 - 3x en y = x - 3. Om de coördinaten van de snijpunten van deze lineaire en kwadratische formule te vinden volg je het volgende stappenplan.
- Stap 1: Om de x-coördinaat van de snijpunten te vinden stel je de twee formules aan elkaar gelijk en los je deze vergelijking op.
x2- 3x = x - 3
x2 - 4x + 3 = 0
(x - 3)(x - 1) = 0
x = 3 ∨ x = 1
De x-coördinaat van het ene snijpunt is dus 1 en van het andere snijpunt 3
- Stap 2: Om de y-coördinaat van de snijpunten te vinden vul je de gevonden waarden voor x in in één van de formules. Handig is om de eenvoudigste formule te gebruiken.
y = x - 3
y = 1 - 3 = -2Snijpunt A is dus (1,-2)
y = x - 3
y = 3 - 3 = 0Snijpunt B is dus (3,0)
Vuistregels
Berekenen van snijpunten van twee formules:
- Stel de vergelijkingen gelijk aan elkaar.
- Los de vergelijking op en bereken daarmee de x-coördinaten van de snijpunten.
- Door de x-coördinaten in te voeren in één van de twee formules, vind je de y-coördinaten.
Voorbeeldvraag
Gegeven zijn de formules y = x2 + 2x en y = -3x - 6.
De grafieken snijden elkaar twee keer. Bereken de coördinaten van de twee verschillende snijpunten.
Uitwerking
Stap 1: Om de x-coördinaat van de snijpunten te vinden stel je de twee formules aan elkaar gelijk en los je deze vergelijking op.
x2+ 2x = -3x - 6
x2 + 2x + 3x + 6 = 0
x2 + 5x + 6 = 0
(x + 2)(x + 3) = 0
x + 2 = 0 ∨ x + 3 = 0
x = -2 ∨ x = -3
De x-coördinaten zijn -2 en -3.
Stap 2: Om de y-coördinaat van de snijpunten te vinden vul je de gevonden waarden voor x in in één van de formules.
x-coördinaten invullen in -3x -6:
x = -2 geeft -3 · -2 - 6 = 0. Dit geeft snijpunt A de coördinaten (-2, 0).
x = -3 geeft -3 · -3 - 6 = 3. Dit geeft snijpunt B de coördinaten (-3, 3).
x-coördinaten invullen in x2+ 2x:
x = -2 geeft -22 + 2 · -2 = 0
x = -3 geeft -32 + 2 · -3 = 3
Zoals je ziet geven beide formules dezelfde coördinaten! Je hoeft de x-coördinaten slechts in één van de formules in te vullen om de y-coördinaten te verkrijgen.
