Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Afstanden bepalen
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Afstanden bepalen eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Afstanden bepalen
Theorie
.png)
Uitdaging
Met behulp van lijnen en cirkels kun je afstanden bepalen. Hiervoor maak je gebruik van de eigenschappen van cirkels en lijnen.
In deze theorie gaan we hier verder op in.
Methode
Cirkels en afstanden
De notatie ⊙(M, 3 cm) houdt in dat er sprake is van een cirkel met middelpunt M en een straal van 3 cm. Elk punt op de cirkel heeft een afstand van 3 cm tot het middelpunt. Voor het binnengebied binnen de cirkel geldt dat ieder punt minder dan 3 cm van het middelpunt M af ligt. Voor het buitengebied geldt dat ieder punt meer dan 3 cm van M af ligt. Als er sprake is van een assenstelsel kan de lengte-eenheid (bijvoorbeeld 'cm') weggelaten worden, dan tellen we vaak in aantal blokjes in plaats van centimeters.
Lijnen en afstanden
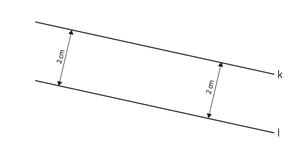
De lijnen k en l zijn evenwijdig aan elkaar. Dit komt omdat elk punt op lijn l een afstand heeft van 2 centimeter tot lijn k.
Ook lijnen kunnen een binnengebied en een buitengebied hebben.
Stel, je hebt lijn q en je wilt het gebied weten, waarbinnen alle punten maximaal 1 centimeter van lijn q liggen. Dan teken je aan beide kanten van lijn q een evenwijdige lijn, op afstand van 1 centimeter. Alle punten tussen deze 2 lijnen in zijn het binnengebied en alle punten buiten deze lijnen zijn het buitengebied.
Net als bij cirkels bestaat er voor lijnen en afstanden ook een notatie.
De notatie d(P, q) = a cm houdt in dat er sprake is van lijn q, met aan beide kanten een evenwijdige lijn op een afstand van a cm. Alle punten P die een afstand van a cm hebben tot lijn l liggen op de evenwijdige lijnen.
Stel zoals hierboven, je hebt lijn q, met 2 evenwijdige lijnen op een afstand van 1 centimeter. Dan geldt dat alle punten P die een afstand van 1 cm hebben tot lijn l op de evenwijdige lijnen liggen.
d(P, q) = 1 centimeter
Voor het binnengebied geldt dat alle punten P op een afstand van q liggen die kleiner is dan 1 cm, dus d(P, q) < 1 cm.
Voor het buitengebied geldt dat alle punten P op een afstand van q liggen die groter is dan 1 cm, dus d(P, q) > 1 cm.
Vuistregels
- ⊙(M, 3 cm) betekent een cirkel met middelpunt M en een straal van 3 cm.
- d(P, q) = a cm betekent een lijn q waarvan alle punten P op a cm van lijn q liggen.
Voorbeeldvraag
a. Gegeven zijn de punten A(-2,1) en B(2,-1). Teken een assenstelsel met deze punten erin. Arceer het gebied waarvan de afstand tot A kleiner is dan 3 en de afstand tot B kleiner dan 4.
b. Gegeven zijn de punten A(-1,0), B(1,2) en C(-1,1). Door AB gaat de lijn l en ⊙(C, 2 cm). Teken deze punten en de lijn in een assenstelsel. Arceer het gebied met afstand tot C < 2 cm en afstand tot de lijn l < 1 cm.
Uitwerking:
a. Zie de uitwerking in figuur 1. Teken allereerst een assenstelsel en zet hier de punten A en B in. Teken dan heb gebied waarin de afstand tot A kleiner is dan 3. Dit doe je door een cirkel met straal 3 te tekenen met als middelpunt punt A.
De tweede voorwaarde is dat de afstand tot punt B kleiner is dan 4. Maak daarom ook een cirkel met een straal van 4 en als middelpunt punt B. Het gebied dat aan beide voorwaarden voldoet is het antwoord op deze vraag.
b. Zie uitwerking in figuur 2. Teken een assenstelsel en zet hier de punten in. Trek vervolgens lijn AB. Je bent opzoek naar punten die een afstand van minder dan cm van punt C afliggen. Hiervoor maak je een cirkel met straal 2 en punt C als middelpunt. De tweede voorwaarde is dat de punten maximaal 1 centimeter van lijn AB afliggen. Hiervoor teken je aan beide kanten van de lijn een evenwijdige lijn die 1 centimeter van lijn AB afligt. Het gebied dat zowel binnen de lijnen als binnen de cirkel ligt, is het gebied dat wij zoeken.
