Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Gevorderd - kwadratische formules
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Gevorderd - kwadratische formules eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Gevorderd - kwadratische formules
Theorie
Uitdaging
Hoe reken je met kwadratische formules?
Methode
Een kwadraat wordt gegeven met een hoge 2 boven een getal, zoals 72.
Het kwadraat bereken je door het getal met zichzelf te vermenigvuldigen:
72 = 7 ⋅ 7 = 49
Het kwadraat van een negatief getal bereken je op dezelfde manier, maar met haakjes om het getal heen:
(-6)2 = -6 ⋅ -6 = 36
Let op: vergeet de haakjes niet.
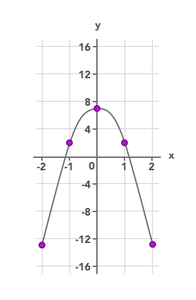
In de afbeelding hiernaast is een parabool getekend met de formule: y = -5x² + 7. Maak de onderstaande tabel af.
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} x & -2 & -1 & 0 & 1 & 2 \T \\\hline y=-5x^2+7 \T & a & b & c & d & e \end{array}$$
a = -5 ⋅ (-2)² + 7 = -5 ⋅ (-2 ⋅ -2) + 7 = -5 ⋅ 4 + 7 = -20 + 7 = -13
b = -5 ⋅ (-1)² + 7 = -5 ⋅ (-1 ⋅ -1) + 7 = -5 ⋅ 1 + 7 = -5 + 7 = 2
c = -5 ⋅ (0)² + 7 = -5 ⋅ 0 + 7 = 7
d = -5 ⋅ (1)² + 7 = -5 ⋅ (1 ⋅ 1) + 7 = -5 ⋅ 1 + 7 = -5 + 7 = 2
e = -5 ⋅ (2)² + 7 = -5 ⋅ (2 ⋅ 2) + 7 = -5 ⋅ 4 + 7 = -20 + 7 = -13
Welke y hoort bij het hoogste punt van de parabool? (Hint: gebruik de bovenstaande tabel om de bijbehorende grafiek te tekenen).
Uit de grafiek blijkt dat het hoogste punt op de y-as ligt. De y-coördinaat kan je meteen aflezen uit de grafiek of je kunt dit berekenen. Een punt dat op de y-as ligt heeft een x-coördinaat gelijk aan 0. Dit betekent dat x = 0.
y = -5 ⋅ (0)² + 7 = -5 ⋅ 0 + 7 = 7
Het hoogste punt heeft dus y = 7.
