Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Rechthoekige driehoek?
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Rechthoekige driehoek? eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Rechthoekige driehoek?
Theorie
Uitdaging
Hoe bepaal je of een driehoek rechthoekig is?
Methode
Een rechthoekige driehoek heeft altijd een rechte hoek. Dit is een hoek van 90 graden. De stelling van Pythagoras geldt in een driehoek met een rechte hoek. Bekijk het voorbeeld hieronder:
Een driehoek heeft de zijden 7 cm, 24 cm en 25 cm. Is deze driehoek een rechthoekige driehoek?
Gebruik de stelling van Pythagoras:
Eerste rechthoekszijde2 + tweede rechthoekszijde2 = schuine zijde2
De langste zijde is de schuine zijde. In dit geval is de schuine zijde 25 cm.
72 + 242 = 252
49 + 576 = 625
Dit is correct, dus dit is een rechthoekige driehoek.
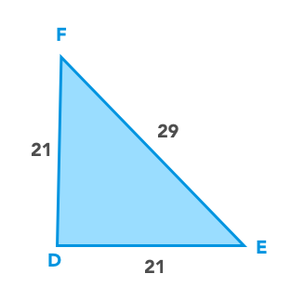
Bekijk de afbeelding hiernaast en bepaal of dit een rechthoekige driehoek is. Zo ja, welke hoek is de rechte hoek?
Gebruik de stelling van Pythagoras. De langste zijde is de schuine zijde. In dit geval is de schuine zijde 29 cm. Vul dit in de formule.
202 + 212 = 292
400 + 441 = 841
Dit is correct, dus dit is een rechthoekige driehoek.
De rechte hoek bevindt zich tegenover de schuine zijde. Tegenover de schuine zijde EF is hoek D. Hoek D is de rechte hoek.
