Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Grafieken en formules
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Grafieken en formules eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Grafieken en formules
Theorie
Uitdaging
Hoe reken je met een formule en hoe teken je de bijbehorende grafiek?
Methode
Bekijk het volgende voorbeeld:
Ibrahim krijgt in de supermarkt elke keer 11 spaarzegels. Thuis heeft hij al 30 spaarzegels liggen. Hierbij hoort de formule S = 30 + 11k, waarbij S het aantal spaarzegels zijn en k het aantal keer dat Ibrahim naar de supermarkt gaat.
a) Hoeveel spaarzegels heeft Ibrahim gespaard na 6 keer naar de supermarkt te zijn gegaan?
In dit geval is k = 6 en kunnen wij dit invullen in de formule:
S = 30 + 11·6
S = 30 + 66
S = 96
Ibrahim heeft 96 spaarzegels gespaard.
b) Vul de onderstaande tabel in en TEKEN de grafiek (ga op de horizontale as tot 20).
$$\newcommand\T{\Rule{0pt}{1em}{.3em}} \begin{array}{c|c|c|c} \mbox{w} & 0 & 5 & 10 & 15 & 20 \T \\\hline \mbox{S} \T & (a) & (b) & (c) & (d) & (e) \end{array}$$
Reken voor elke k de bijbehorende S uit.
(a) = 30 + 11·0 = 30
(b) = 30 + 11·5 = 85
(c) = 30 + 11·10 = 140
(d) = 30 + 11·15 = 195
(e) = 30 + 11·20 = 250
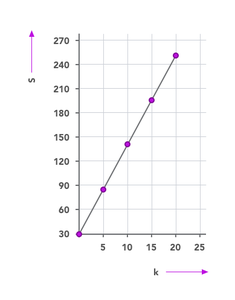
Teken alle punten die zijn gegeven in de tabel in de grafiek. Nu kun je lijnen tussen de punten trekken en ontstaat er de grafiek die je ziet in de afbeelding.
c) Wat is het stijggetal en begingetal bij deze formule?
Ibrahim heeft thuis al 30 spaarzegels liggen, dus het begingetal is 30. Elke keer als hij naar de supermarkt gaat krijgt Ibrahim 11 spaarzegels erbij, het aantal spaarzegels stijgt met 11. Dus het stijggetal is 11.
