Het meest gebruiksvriendelijke oefenprogramma vól slimmigheden
Gevorderd - omtrek en oppervlakte van een cirkel
Met Slimleren oefenen leerlingen thuis of in de les, op een leuke en interactieve manier, de stof die jij voor ze klaar zet. Benieuwd naar onze stof? Hieronder zie je hoe het onderwerp Gevorderd - omtrek en oppervlakte van een cirkel eruit ziet. Leerlingen kunnen in Slimleren vragen over dit - en ieder ander - onderwerp maken. Docenten kunnen de resultaten daarvan inzien en daarmee hun lessen efficiënter inrichten en makkelijker differentiëren.
Gevorderd - omtrek en oppervlakte van een cirkel
Theorie
Uitdaging
Bij cirkelvormige figuren kun je geen lengte en breedte aanwijzen om de omtrek en oppervlakte te bepalen. Je moet hiervoor dus op een andere manier te werk gaan dan bij rechthoekige figuren.
Bij het berekenen van de omtrek en oppervlakte van een cirkel zijn de diameter, de straal en het getal pi belangrijk.
Methode
Diameter
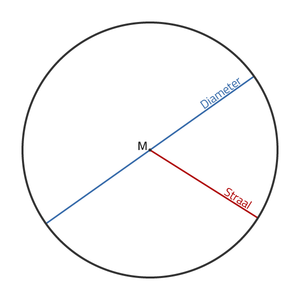
Bij cirkels kijken we naar de diameter, of de doorsnede. In de figuur zie je een cirkel met de diameter. Zoals je ziet loopt de diameter precies door het middelpunt van de cirkel.
Straal
In de figuur zie je ook de straal. De straal is de helft van de diameter en loopt vanaf het middelpunt naar de buitenrand van de cirkel.
De straal weergeven we met het symbool r.
De omtrek
Pi is een getal en geven we weer met het symbool: $$\pi$$
- $$\pi$$ heeft oneindig veel cijfers achter de komma en wordt daarom afgerond tot $$\approx$$ 3,14. In de rekenmachine kunnen we $$\pi$$ intoetsen.
De omtrek van een cirkel berekenen we met de volgende standaardformule:
- Omtrek = $$\pi$$ · diameter
De omtrek kan ook worden uitgerekend met de straal. We weten namelijk dat de straal de helft van de diameter is. Dus 2 keer de straal is hetzelfde als de diameter.
- De diameter = 2 · straal = 2 · r
- Omtrek = $$\pi$$ · 2 · r
De oppervlakte
De oppervlakte van een cirkel berekenen we met de volgende standaardformule:
Oppervlakte cirkel = $$\pi$$ · straal2
Zoals je ziet heb je twee waarden nodig om de oppervlakte van een cirkel te kunnen berekenen:
- $$\pi$$, dit Griekse getal noemen we pi. Dit is een getal met eindeloos veel cijfers achter de komma (= 3,14...).
- De straal, ofwel de radius, r. Dit is de helft van de diameter. De diameter is de doorsnede van een cirkel (zie de afbeelding). Als de straal niet gegeven is maar de diameter van de cirkel wel gegeven is, dan bereken je de straal als volgt: $${r =} \frac{1}{2} · \mbox{diameter} $$
Vuistregels
- $$\pi$$ = 3,1415926....... $$\approx$$ 3,14
- Straal = r
- Diameter = 2 · straal = 2 · r
- Omtrek =$$\pi$$ · 2 · r = $$\pi$$ · diameter
- Oppervlakte = $$\pi$$ · r 2
Voorbeeldvraag
a. De diameter van een wiel is 65 cm. Bereken de omtrek van het wiel in cm, in 1 decimaal nauwkeurig.
b. Robert fietst 1,7 km naar school. Hoeveel keer heeft het wiel rond gedraaid? Rond af op hele getallen.
c. De straal van een emmer is 15 cm. Bereken de omtrek van de emmer in cm, in twee decimalen nauwkeurig.
Uitwerking:
a. We weten dat de omtrek = $$\pi$$ · diameter. De diameter is gegeven.
Omtrek = $$\pi$$ · 65 = 204,2 cm.
b. We weten de omtrek van de cirkel (het wiel). Deze is 204,2 cm.
De afstand die Robert aflegt is 1,7 km. Hoe vaak het wiel ronddraait berekenen we door te kijken hoeveel keer de omtrek in de afstand van 1,7 km past. Dat is het aantal keer dat het wiel moet rond draaien.
Eerst rekenen we alles om naar dezelfde eenheid. We hebben hier gekozen voor meter.
1,7 km = 1.700 m
204,2 cm = 2,042 m
Nu kunnen we het aantal rondes berekenen:
Aantal keer rond gedraaid = 1.700 : 2,042 = 833 hele rondes
c. De straal is gegeven. We weten dat 2 keer de straal is gelijk aan de diameter. Zo kunnen we de omtrek berekenen.
Omtrek = $$\pi$$ · 2 · 15 = 94,25 cm.
