Welke lesstof is er beschikbaar in het programma van Slimleren?

 

Hyperbool - omgekeerd evenredig verband

Uitdaging

In de wiskunde komen we constant grootheden en eenheden tegen. Tussen grootheden kunnen verbanden bestaan. De verbanden kunnen evenredig, niet-evenredig of omgekeerd evenredig zijn.

Wat deze begrippen betekenen leggen we je uit in deze theorie.

Methode

In de wereld kun je van alles meten. We meten dagelijks de temperatuur, je weegt jezelf, je meet je lengte, enzovoort. Deze dingen die je kunt meten zijn allemaal voorbeelden van grootheden. Deze grootheden worden op hun beurt weer weergegeven in eenheden. De grootheid lengte meet je in centimeters. Een centimeter is de eenheid van lengte. Tussen grootheden kunnen verbanden bestaan.

Zo kan er tussen een tweetal grootheden een evenredig verband zijn. Dit houdt in dat als je de ene grootheid met een getal vermenigvuldigt, je de andere grootheid ook met dit getal vermenigvuldigt.

Neem bijvoorbeeld het aantal punten dat je haalt op een toets en het cijfer voor die toets. Stel je haalt met 20 punten een 5 als cijfer, en met 40 punten een 10 als cijfer. Dan heb je te maken met een evenredig verband, omdat je met 2x zoveel punten ook een 2x zo hoog cijfer haalt.

Ook kan er tussen een tweetal grootheden een omgekeerd evenredig verband zijn. Dit houdt in dat als je de ene grootheid met een getal vermenigvuldigt, je de andere grootheid juist moet delen door dit getal.

In een supermarkt zijn twee vakkenvullers aan het werk. Zij moeten 10 kisten met producten in de schappen zetten. Hier doen zij samen 6 uur over. Stel nou dat er 4 vakkenvullers aan het werk waren, in plaats van 2. Dan konden zij het werk in 3 uur afkrijgen. Dus vermenigvuldig je het aantal vakkenvullers met 2, dan deel je het aantal uur werk door 2. Het aantal vakkenvullers is omgekeerd evenredig met het aantal uur werk.

Een ander voorbeeld is een huis dat wordt verbouwd, waarbij x het aantal bouwers is en y is het aantal dagen dat de verbouwing gaat duren. Als er meer bouwers meewerken, x neemt toe, dan gaat het aantal dagen dat de verbouwing gaat duren om laag, y neemt af. Als x toeneemt terwijl y evenredig afneemt spreken we van een omgekeerd evenredig verband.

Als twee grootheden omgekeerd evenredig zijn, dan is de vermenigvuldiging van de grootheden altijd hetzelfde getal.

De standaard formule is $$y =\frac{a}{x}$$

Wanneer een verband omgekeerd evenredig is, is a altijd een vast getal.

Wanneer x 2 keer zo klein is, is y 2 keer zo groot.

Oftewel samengevat:

• Vermenigvuldig je x met een getal k, dan moet je y door het getal k delen.
• x · y = a, waarbij a constant is.

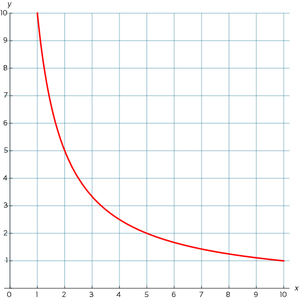
Omgekeerd evenredig verband wordt ook wel hyperbolisch verband genoemd, omdat de grafiek die hierbij hoort een hyperbool heet. Een voorbeeld van z'n grafiek zie je in de afbeelding.